
【题目】已知抛物线C:![]() (
(![]() )的焦点F到准线l的距离为2,直线
)的焦点F到准线l的距离为2,直线![]() 过点F且与抛物线交于M、N两点,直线
过点F且与抛物线交于M、N两点,直线![]() 过坐标原点O及点M且与l交于点P,点Q在线段
过坐标原点O及点M且与l交于点P,点Q在线段![]() 上.
上.
(1)求直线![]() 的斜率;
的斜率;
(2)若![]() ,
,![]() ,
,![]() 成等差数列,求点Q的轨迹方程.
成等差数列,求点Q的轨迹方程.
 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直线PB与CD所成角的大小为![]() ,求BC的长;
,求BC的长;
(Ⅱ)求二面角B-PD-A的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某公司一种产品的日销售量![]() (单位:百件)关于日最高气温
(单位:百件)关于日最高气温![]() (单位:
(单位:![]() )的散点图.
)的散点图.

数据:
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
(1)请剔除一组数据,使得剩余数据的线性相关性最强,并用剩余数据求日销售量![]() 关于日最高气温
关于日最高气温![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据现行《重庆市防暑降温措施管理办法》.若气温超过36度,职工可享受高温补贴.已知某日该产品的销售量为53.1,请用(1)中求出的线性回归方程判断该公司员工当天是否可享受高温补贴?
附: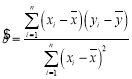 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() 的焦距为
的焦距为![]() ,直线
,直线![]() (
(![]() )与
)与![]() 交于两个不同的点
交于两个不同的点![]() 、
、![]() ,且
,且![]() 时直线
时直线![]() 与
与![]() 的两条渐近线所围成的三角形恰为等边三角形.
的两条渐近线所围成的三角形恰为等边三角形.
(1)求双曲线![]() 的方程;
的方程;
(2)若坐标原点![]() 在以线段
在以线段![]() 为直径的圆的内部,求实数
为直径的圆的内部,求实数![]() 的取值范围;
的取值范围;
(3)设![]() 、
、![]() 分别是
分别是![]() 的左、右两顶点,线段
的左、右两顶点,线段![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:线段
,求证:线段![]() 在
在![]() 轴上的射影长为定值.
轴上的射影长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为![]() 的数列
的数列![]() 各项均为正数,且
各项均为正数,且![]() ,
,![]() .
.
(1)若数列![]() 的通项
的通项![]() 满足
满足![]() ,且
,且![]() ,求数列
,求数列![]() 的前n项和为
的前n项和为![]() ;
;
(2)若数列![]() 的通项
的通项![]() 满足
满足 ,前n项和为
,前n项和为![]() ,当数列
,当数列![]() 是等差数列时,对任意的
是等差数列时,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求满足条件的所有整数
成立,求满足条件的所有整数![]() 构成的集合.
构成的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海域有![]() 两个岛屿,
两个岛屿,![]() 岛在
岛在![]() 岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线
岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线![]() ,曾有渔船在距
,曾有渔船在距![]() 岛、
岛、![]() 岛距离和为8海里处发出过鱼群。以
岛距离和为8海里处发出过鱼群。以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 的垂直平分线为
的垂直平分线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求曲线![]() 的标准方程;
的标准方程;
(2)某日,研究人员在![]() 两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),
两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),![]() 两岛收到鱼群在
两岛收到鱼群在![]() 处反射信号的时间比为
处反射信号的时间比为![]() ,问你能否确定
,问你能否确定![]() 处的位置(即点
处的位置(即点![]() 的坐标)?
的坐标)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com