
空间四边形PABC中,PA、PB、PC两两相互垂直,∠PBA=45°,∠PBC=60°,M为AB的中点.

(1)求BC与平面PAB所成的角;
(2)求证:AB⊥平面PMC.
|
解:∵PA⊥AB,∴∠APB=90° 在RtΔAPB中,∵∠ABP=45°,设PA=a, 则PB=a,AB= ∵∠PBC=60°,PB=a.∴BC=2a,PC= ∵AP⊥PC ∴在RtΔAPC中,AC= (1)∵PC⊥PA,PC⊥PB,∴PC⊥平面PAB, ∴BC在平面PBC上的射影是BP. ∠CBP是CB与平面PAB所成的角 ∵∠PBC=60°,∴BC与平面PBA的角为60°. (2)由上知,PA=PB=a,AC=BC=2a. ∴M为AB的中点,则AB⊥PM,AB⊥CM. ∴AB⊥平面PCM. 说明:要清楚线面的垂直关系,线面角的定义,通过数据特点,发现解题捷径. |
|
此题数据特殊,先考虑数据关系及计算、发现解题思路. |


科目:高中数学 来源: 题型:
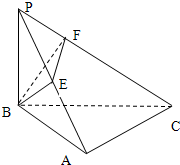 如图,空间四边形PABC中,PB⊥底面ABC,∠BAC=90°;过点B作BE,BF分别垂直于AP,CP于点E,F.
如图,空间四边形PABC中,PB⊥底面ABC,∠BAC=90°;过点B作BE,BF分别垂直于AP,CP于点E,F.查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分) 如图,空间四边形PABC中,PB⊥底面ABC,∠BAC=90°;过点B作BE,
 BF分别垂直于AP,CP于点E,F。
BF分别垂直于AP,CP于点E,F。
(1) 求证:AC⊥面PAB;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2) 求证:PC⊥EF。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com