【题目】四棱柱
的底面ABCD为矩形，AB＝1，AD＝2，
，
，则
的长为( )
A． 
B． 
C． 
D．
【答案】C
【解析】分析：记A1在面ABCD内的射影为O，O在∠BAD的平分线上，说明∠BAD的平分线即菱形ABCD的对角线AC，求AC1的长．
解答：解：记A1在面ABCD内的射影为O，
∵∠A1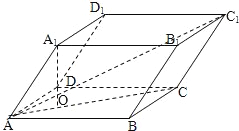
AB=∠A1AD，
∴O在∠BAD的平分线上，
由O向AB，AD两边作垂线，垂足分别为E，F，连接A1E，A1F，A1E，A1F分别垂直AB，AD于E，F
∵AA1=3，∠A1AB=∠A1AD=60°，
∴AE=AF=
又四棱柱ABCD-A1B1C1D1的底面ABCD为矩形
∴∠OAF=∠OAE=45°，且OE=OF=
，可得OA=
在直角三角形A1OA中，由勾股定理得A1O=
过C1作C1M垂直底面于M，则有△C1MC≌△A1OA，由此可得M到直线AD的距离是
，M到直线AB的距离是
，C1M=A1O=
所以AC1 =
=
故选C．
一本好题口算题卡系列答案科目：高中数学 来源： 题型：
【题目】某学校为调查高二学生上学路程所需要的时间（单位：分钟），从高二年级学生中随机抽取
名按上学所需要时间分组：第
组
，第
组
，第
组
，第
组
，第
组
，得到的频率分布直方图如图所示．
（
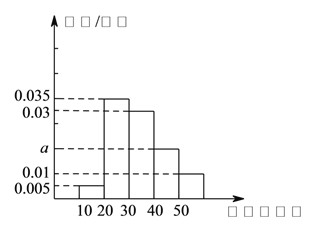
）根据图中数据求
的值．
（
）若从第
， 
， 
组中用分层抽样的方法抽取
名新生参与交通安全问卷调查，应从第
， 
， 
组各抽取多少名新生？
（
）在（
）的条件下，该校决定从这
名学生中随机抽取
名新生参加交通安全宣传活动，求第
组至少有一志愿者被抽中的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=lnx﹣mx+m，m∈R．
（1）求函数f（x）的单调区间．
（2）若f（x）≤0在x∈（0，+∞）上恒成立，求实数m的取值范围．
（3）在（2）的条件下，任意的0＜a＜b， 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xoy中，已知直线l：x+y+a=0与点A（0，2），若直线l上存在点M满足|MA|2+|MO|2=10（O为坐标原点），则实数a的取值范围是（ ）
A.（﹣ 
﹣1， ﹣1）
B.[﹣ ﹣1， ﹣1]
C.（﹣2 
﹣1，2 ﹣1）
D.[﹣2 ﹣1，2 ﹣1]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】.如图，已知
，图中的一系列圆是圆心分别为A、B的两组同心圆，每组同心圆的半径分别是1，2，3，…，n，….利用这两组同心圆可以画出以A、B为焦点的双曲线. 若其中经过点M、N、P的双曲线的离心率分别是
.则它们的大小关系是 （用“
”连接）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ex﹣ax﹣1（a为常数），曲线y=f（x）在与y轴的交点A处的切线斜率为﹣1．
（1）求a的值及函数y=f（x）的单调区间；
（2）若x1＜ln2，x2＞ln2，且f（x1）=f（x2），证明：x1+x2＜2ln2．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若集合A={x|x2＜2x}，集合B={x|x＜ 
}，则A∩（RB）等于（ ）
A.（﹣2， 
]
B.（2，+∞）
C.（﹣∞， ]
D.D[ ，2）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法中正确的是（ ）
A. 
时，函数
是增函数，因为
，所以
是增函数，这种推理是合情合理.
B. 在平面中，对于三条不同的直线
， 
， 
，若
， 
，将此结论放在空间中也是如此，这种推理是演绎推理.
C. 命题
： 
， 
的否定是
： 
， 
.
D. 若分类变量
与
的随机变量
的观察值越小，则两个分类变量有关系的把握性越小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
