Question

【题目】已知函数

(1)求函数的最大值和最小值,并求取得最大值和最小值时对应的的值；

(2)设方程在区间内有两个相异的实数根求的值；

(3)如果对于区间上的任意一个都有成立,求实数的取值范围.

Answer 1

【答案】（1）f（x）的最大值为2，此时x＝kπ，k∈Z，f（x）的最小值为﹣2，此时x＝kπ，k∈Z；（2）x1+x2＝或x1+x2＝；（3）a≥1．

【解析】

（1）利用三角形的恒等变换，将f（x）化简成f（x）＝2sin（2x），再求f（x）的最大值和最小值，

（2）根据函数图象，找到m的取值范围，观察x1和x2的关系，写出x1+x2的值，

（3）根据定义域求得f（x）的取值范围，再求a的取值范围．

（1）f（x）＝2sin（π+x）sin（x）+2cos2x﹣1，

sin2x+cos2x，

＝2sin（2x），

f（x）的最大值为2，x取得最大值对应的x的值x＝kπ，k∈Z，

f（x）的最小值为﹣2，x取得最小值对应x的值x＝kπ，k∈Z，

（2）f（x）＝m，sin（2x），

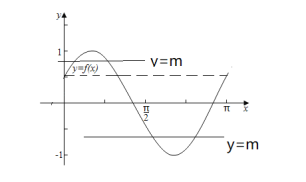
f（x）＝m在（0，π）内有相异的两个实数根x1，x2，f（x）与有两个不同的交点，

或，

由图象可知：当m∈（1，）函数y＝f（x）的图象关于直线x对称，

x1+x2＝2；

当m∈（-1，），函数y＝f（x）的图象关于直线x对称，

x1+x2＝2，综上x1+x2＝或x1+x2＝

（3）f（x）﹣a≤1，即a≥f（x）﹣1，

x∈[，]，2x∈[，]，

∴f（x）∈[﹣1，2]，

∴a≥1．