
【题目】在极坐标系中,方程C:![]() 表示的曲线被称作“四叶玫瑰线”(如图)
表示的曲线被称作“四叶玫瑰线”(如图)

(1)求以极点为圆心的单位圆与四叶玫瑰线交点的极坐标和直角坐标;
(2)直角坐标系的原点与极点重合,x轴正半轴与极轴重合.求直线l:![]() 上的点M与四叶攻瑰线上的点N的距离的最小值.
上的点M与四叶攻瑰线上的点N的距离的最小值.
【答案】(1)极坐标为![]() ,直角坐标为
,直角坐标为![]() ;(2)
;(2)![]()
【解析】
(1)先求出以极点为圆心的单位圆的极坐标方程,与玫瑰线方程联立即可求出交点的极坐标;
(2)首先可得四叶玫瑰线关于直线![]() 对称,将直线方程转化为普通方程,直线
对称,将直线方程转化为普通方程,直线![]() 与直线
与直线![]() 垂直,且玫瑰线在直线
垂直,且玫瑰线在直线![]() 的同侧,即可得到距离的最小值;
的同侧,即可得到距离的最小值;
解:(1)因为![]()
![]()
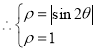
![]()
![]()
所以![]() ,
,![]()
取![]() ,得
,得![]()
从而得到单位圆与四叶玫瑰线交点的极坐标为![]() ,
,
化成直角坐标就是![]()
(2)直观发现,四叶玫瑰线关于直线![]() 对称.
对称.
事实上,将极坐标方程![]() 化作直角坐标方程得
化作直角坐标方程得![]() ,
,
将![]() 互换后方程不变,说明四叶玫瑰线关于直线
互换后方程不变,说明四叶玫瑰线关于直线![]() 对称;
对称;
将![]() 换作
换作![]() ,
,![]() 换作
换作![]() 后方程不变,说明四叶玫瑰线关于直线
后方程不变,说明四叶玫瑰线关于直线![]() 对称;
对称;
直线![]() 的普通方程是
的普通方程是![]() ,
,
直线![]() 与直线
与直线![]() 垂直,且玫瑰线在直线
垂直,且玫瑰线在直线![]() 的同侧,
的同侧,
故![]() 的最小值等于点
的最小值等于点![]() 到直线
到直线![]() 的距离:
的距离:
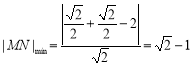 .
.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,侧面PAD是边长为2的等边三角形且垂直于底![]() ,
, ![]()
![]() 是
是![]() 的中点。
的中点。
(1)证明:直线![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家,大约公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,又称“赵爽弦图”(以弦为边长得到的正方形是由![]() 个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由
个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由![]() 个全等的三角形与中间的一个小正六边形组成的一个大正六边形,设
个全等的三角形与中间的一个小正六边形组成的一个大正六边形,设![]() ,若在大正六边形中随机取一点,则此点取自小正六边形的概率为( )
,若在大正六边形中随机取一点,则此点取自小正六边形的概率为( )
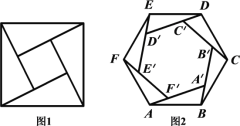
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节前后,一场突如其来的新冠肺炎疫情在武汉出现并很快地传染开来(已有证据表明2019年10月、11月国外已经存在新冠肺炎病毒),人传人,传播快,传播广,病亡率高,对人类生命形成巨大危害.在中华人民共和国,在中共中央、国务院强有力的组织领导下,全国人民万众一心抗击、防控新冠肺炎,疫情早在3月底已经得到了非常好的控制(累计病亡人数3869人).然而,国外因国家体制、思想观念与中国的不同,防控不力,新冠肺炎疫情越来越严重.据美国约翰斯·霍普金斯大学每日下午6时公布的统计数据,选取5月6日至5月10日的美国的新冠肺炎病亡人数如下表(其中t表示时间变量,日期“5月6日”、“5月7日”对应于“t=6"、“t=7",依次下去),由下表求得累计病亡人数与时间的相关系数r=0.98.
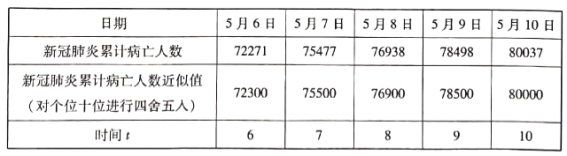
(1)在5月6日~10日,美国新冠肺炎病亡人数与时间(日期)是否呈现线性相关性?
(2)选择对累计病亡人数四舍五入后个位、十位均为0的近似数,求每日累计病亡人数y随时间t变化的线性回归方程;
(3)请估计美国5月11日新冠肺炎病亡累计人数,请初步预测病亡人数达到9万的日期.
附:回归方程![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为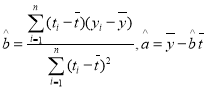
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
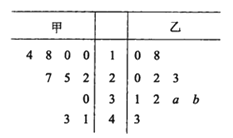
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)当![]() 时,记甲型号电视机的“星级卖场”数量为
时,记甲型号电视机的“星级卖场”数量为![]() ,乙型号电视机的“星级卖场”数量为
,乙型号电视机的“星级卖场”数量为![]() ,比较
,比较![]() 的大小关系;
的大小关系;
(2)在这10个卖场中,随机选取2个卖场,记![]() 为其中甲型号电视机的“星级卖场”的个数,求
为其中甲型号电视机的“星级卖场”的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若![]() ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为![]() ,根据茎叶图推断
,根据茎叶图推断![]() 为何值时,
为何值时,![]() 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() .由集合P中所有的点组成的图形如图中阴影部分所示,中间白色部分形如美丽的“水滴”.给出下列结论:
.由集合P中所有的点组成的图形如图中阴影部分所示,中间白色部分形如美丽的“水滴”.给出下列结论:

①“水滴”图形与y轴相交,最高点记为A,则点A的坐标为![]() ;
;
②在集合P中任取一点M,则M到原点的距离的最大值为3;
③阴影部分与y轴相交,最高点和最低点分别记为C,D,则![]() ;
;
④白色“水滴”图形的面积是![]() .
.
其中正确的有______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国女排,曾经十度成为世界冠军,铸就了响彻中华的女排精神.女排精神的具体表现为:扎扎实实,勤学苦练,无所畏惧,顽强拼搏,同甘共苦,团结战斗,刻苦钻研,勇攀高峰.女排精神对各行各业的劳动者起到了激励、感召和促进作用,给予全国人民巨大的鼓舞.
(1)看过中国女排的纪录片后,某大学掀起“学习女排精神,塑造健康体魄”的年度主题活动,一段时间后,学生的身体素质明显提高,将该大学近5个月体重超重的人数进行统计,得到如下表格:
月份x | 1 | 2 | 3 | 4 | 5 |
体重超重的人数y | 640 | 540 | 420 | 300 | 200 |
若该大学体重超重人数y与月份变量x(月份变量x依次为1,2,3,4,5…)具有线性相关关系,请预测从第几月份开始该大学体重超重的人数降至10人以下?
(2)在某次排球训练课上,球恰由A队员控制,此后排球仅在A队员、B队员和C队员三人中传递,已知每当球由A队员控制时,传给B队员的概率为![]() ,传给C队员的概率为
,传给C队员的概率为![]() ;每当球由B队员控制时,传给A队员的概率为
;每当球由B队员控制时,传给A队员的概率为![]() ,传给C队员的概率为
,传给C队员的概率为![]() ;每当球由C队员控制时,传给A队员的概率为
;每当球由C队员控制时,传给A队员的概率为![]() ,传给B队员的概率为
,传给B队员的概率为![]() .记
.记![]() ,
,![]() ,
,![]() 为经过n次传球后球分别恰由A队员、B队员、C队员控制的概率.
为经过n次传球后球分别恰由A队员、B队员、C队员控制的概率.
(i)若![]() ,B队员控制球的次数为X,求
,B队员控制球的次数为X,求![]() ;
;
(ii)若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,证明:
,证明:![]() 为等比数列,并判断经过200次传球后A队员控制球的概率与
为等比数列,并判断经过200次传球后A队员控制球的概率与![]() 的大小.
的大小.
附1:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: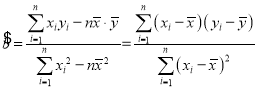 ;
;![]() .
.
附2:参考数据:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com