
【题目】已知a是实数,函数f(x)=![]() (x-a).
(x-a).
(1)求函数f(x)的单调区间;
(2)设g(a)为f(x)在区间[0,2]上的最小值.
①写出g(a)的表达式;
②求a的取值范围,使得-6≤g(a)≤-2.
【答案】见解析
【解析】解 (1)函数的定义域为[0,+∞),
f′(x)=![]() +
+![]() =
=![]() (x>0).
(x>0).
若a≤0,则f′(x)>0,f(x)有单调递增区间[0,+∞).
若a>0,令f′(x)=0,得x=![]() ,
,
当0<x<![]() 时,f′(x)<0,
时,f′(x)<0,
当x>![]() 时,f′(x)>0.
时,f′(x)>0.
f(x)有单调递减区间[0,![]() ],有单调递增区间(
],有单调递增区间(![]() ,+∞).
,+∞).
(2)①由(1)知,若a≤0,f(x)在[0,2]上单调递增,
所以g(a)=f(0)=0.
若0<a<6,f(x)在[0,![]() ]上单调递减,在(
]上单调递减,在(![]() ,2]上单调递增,
,2]上单调递增,
所以g(a)=f(![]() )=-
)=-![]()
![]() .
.
若a≥6,f(x)在[0,2]上单调递减,所以g(a)=f(2)=![]() (2-a).
(2-a).
综上所述,g(a)=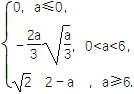
②令-6≤g(a)≤-2.若a≤0,无解.
若0<a<6,解得3≤a<6.
若a≥6,解得6≤a≤2+3![]() .
.
故a的取值范围为3≤a≤2+3![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】每逢节假日,在微信好友群中发红包逐渐成为一种时尚,还能增进彼此的感情,2016年春节期间,小鲁在自己的微信好友群中,向在线的甲、乙、丙、丁四位好友随机发放红包,发放的规则为:每次发放一个,小鲁自己不抢,每个人抢到的概率相同.
(1)若小鲁随机发放了3个红包,求甲至少抢到一个红包的概率;
(2)若丁因有事暂时离线一段时间,而小鲁在这段时间内共发了3个红包,其中2个红包中各有10元,一个红包中有5元.设这段时间内乙所得红包的总钱数为![]() 元,求随机变量
元,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数![]() (m∈Z)为偶函数,且在区间(0,+∞)上是单调增函数.
(m∈Z)为偶函数,且在区间(0,+∞)上是单调增函数.
(1)求函数f(x)的解析式;
(2)设函数![]() ,若g(x)>2对任意的x∈R恒成立,求实数c的取值范围.
,若g(x)>2对任意的x∈R恒成立,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本着健康、低碳的生活理念,租用公共自行车的人越来越多.租用公共自行车的收费标准是每车每次不超过两小时免费,超过两小时的部分每小时2元(不足1小时的部分按1小时计算).甲乙两人相互独立租车(各租一车一次).设甲、乙不超过两小时还车的概率分别为![]() ,
, ![]() ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为![]() ,
, ![]() ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(1)求出甲、乙所付租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量![]() ,求随机变量
,求随机变量![]() 的概率分布和期望.
的概率分布和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a是实数,函数f(x)=![]() (x-a).
(x-a).
(1)求函数f(x)的单调区间;
(2)设g(a)为f(x)在区间[0,2]上的最小值.
①写出g(a)的表达式;
②求a的取值范围,使得-6≤g(a)≤-2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P、Q为两个非空集合,定义集合P+Q={m+n| m∈P,n∈Q},若P={0,2,5}, Q={1,2,6},则P+Q中元素的个数为 ( )
A. 9 B. 8 C. 7 D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下是解决数学问题的思维过程的流程图:
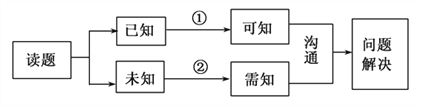
在此流程图中,①、②两条流程线与“推理与证明”中的思维方法匹配正确的是( )
A. ![]() ①—分析法,②—反证法 B. ①—分析法,②—综合法
①—分析法,②—反证法 B. ①—分析法,②—综合法
C. ①—综合法,②—反证法 D. ①—综合法,②—分析法
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆![]() :
: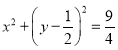 经过椭圆
经过椭圆![]() :
:![]() (
(![]() )的左右焦点
)的左右焦点![]() ,
,![]() ,与椭圆
,与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
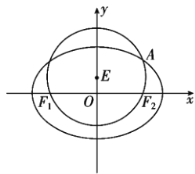
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设与直线![]() (
(![]() 为原点)平行的直线
为原点)平行的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点.当
两点.当![]() 的面积取到最大值时,求直线
的面积取到最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有( )
①函数y=![]() 的定义域为{x|x≥1};
的定义域为{x|x≥1};
②函数y=x2+x+1在(0,+∞)上是增函数;
③函数f(x)=x3+1(x∈R),若f(a)=2,则f(-a)=-2;
④已知f(x)是R上的增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b).
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com