
如图,设向量 ,若
,若 ,且
,且 ,则用阴影表示
,则用阴影表示 点所有可能的位置区域正确的是 ( )
点所有可能的位置区域正确的是 ( )

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
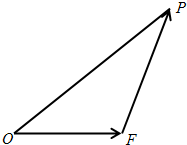 如图,设△OEP的面积为S,已知
如图,设△OEP的面积为S,已知| OF |
| FP |
| 1 |
| 2 |
| ||
| 2 |
| OF |
| FP |
| 3 |
| 4 |
| OF |
| OF |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
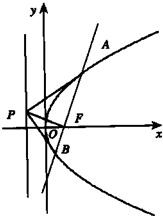 如图,设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,且A、B两点坐标为(x1,y1),(x2,y2),y1>0,y2<0,P是此抛物线的准线上的一点,O是坐标原点.
如图,设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,且A、B两点坐标为(x1,y1),(x2,y2),y1>0,y2<0,P是此抛物线的准线上的一点,O是坐标原点.| PA |
| PB |
查看答案和解析>>
科目:高中数学 来源:模拟题 题型:解答题
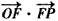 =1,
=1,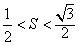 ,求向量
,求向量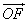 与
与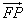 的夹角θ的取值范围;
的夹角θ的取值范围;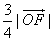 且
且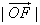 ≥2,当
≥2,当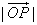 取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程。
取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程。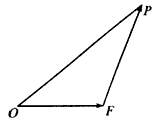
查看答案和解析>>
科目:高中数学 来源:2011年广东省高考数学第三轮复习精编模拟试卷12(理科)(解析版) 题型:解答题
 =1.
=1. ,求向量
,求向量 与
与 的夹角θ的取值范围;
的夹角θ的取值范围; |
| |,且|
|,且| |≥2,当|
|≥2,当| |取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.
|取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com