【题目】已知椭圆
（a＞b＞0）的左、右焦点为F1、F2，点A
在椭圆上，且
与x轴垂直．
（1）求椭圆的方程；
（2）过A作直线与椭圆交于另外一点B，求△AOB面积的最大值．
【答案】（1）
；（2）
.
【解析】
试题分析：本题主要考查了椭圆的标准方程和椭圆与直线等基础知识，考查了学生综合运用所学知识，创造性地解决问题的能力、转化能力、计算能力，解题时要认真审题，仔细解答．第一问，由已知：
，
，解得
，
，从而写出方程；第二问，
斜率不存在或斜率存在两种情况讨论，当的斜率存在时，令直线与椭圆方程联立，消参，利用两点间距离公式和点到直线的距离分别求出
和边上的高，代入到三角形面积公式中，计算三角形面积，求出最大值.
试题解析：（1）有已知：，∴，
，
故椭圆方程为
；
（2）当斜率不存在时：
，
当斜率存在时：设其方程为：
，
由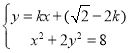
得
，
由已知：
，
即：
，
，
到直线的距离：
，
，
，
，
此时
，
综上所求：当斜率不存在或斜率存在时：
面积取最大值为
．
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，平面
平面
，
，
是等边三角形.已知
，
，
.
（1）设
是
上的一点，证明：平面
平面
；
（2）当
点位于线段
什么位置时，
平面
？
（3）求四棱锥
的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂用7万元钱购买了一台新机器，运输安装费用2千元，每年投保、动力消耗的费用也为2千元，每年的保养、维修、更换易损零件的费用逐年增加，第一年为2千元，第二年为3千元，第三年为4千元，依此类推，即每年增加1千元．问这台机器最佳使用年限是多少年？并求出年平均费用的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
（1）当
时，证明：函数
不是奇函数；
（2）判断函数
的单调性，并利用函数单调性的定义给出证明；
（3）若是奇函数，且
在
时恒成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在空间四边形ABCD中，平面ABD⊥平面BCD，且DA⊥平面ABC，则△ABC是（ ）
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】面对某种流感病毒，各国医疗科研机构都在研究疫苗，现有A、B、C三个独立的研究机构在一定的时期研制出疫苗的概率分别为
．求:
（1）他们能研制出疫苗的概率；
（2）至多有一个机构研制出疫苗的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“孪生函数”，那么函数解析式为y＝2x2－3，值域为{1，5}的“孪生函数”共有（ ）
A.10个
B.9个
C.8个
D.4个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
,在平面直角坐标系中，已知向量
，向量
，动点
的轨迹为
.
（1）求轨迹的方程,并说明该方程所表示曲线的形状；
（2）已知
,证明：存在圆心在原点的圆,使得该圆的任意一条切线与轨迹恒有两个交点
，且
为坐标原点），并求该圆的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】编号1~15的小球共15个,求总体号码的平均值,试验者从中抽3个小球,以它们的平均数估计总体平均数,以编号2为起点,用系统抽样法抽3个小球,则这3个球的编号平均数是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com