
【题目】2002年国际数学家大会在北京召开,会标是以我国古代数学家赵爽的弦图为基础设计.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图)如果小正方形的边长为1,大正方形的边长为5,直角三角形中较小的锐角为![]() ,则
,则![]() ( )
( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像是由函数
的图像是由函数![]() 的图像经如下变换得到:先将
的图像经如下变换得到:先将![]() 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移![]() 个单位长度.
个单位长度.
(Ⅰ)求函数![]() 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于![]() 的方程
的方程![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() .
.
(1)求实数m的取值范围;
(2)证明:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组: ![]()
![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图: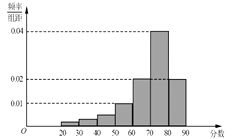
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
(1)求证:B1D1∥平面A1BD;
(2)求证:MD⊥AC;
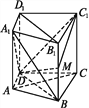
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两艘轮船都要停靠在同一个泊位,它们可能在一昼夜的任意时刻到达.甲、乙两船停靠泊位的时间分别为4小时与2小时,求有一艘船停靠泊位时必需等待一段时间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加书法社团 | 2 | 30 |
(1)从该班随机选 1 名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 8 名同学中,有 5 名男同学![]() ,3名女同学
,3名女同学![]() .现从这 5 名男同学和 3 名女同学中各随机选 1 人,求
.现从这 5 名男同学和 3 名女同学中各随机选 1 人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)
已知正项数列![]() 满足:对任意正整数
满足:对任意正整数![]() ,都有
,都有![]() 成等差数列,
成等差数列,![]() 成等比数列,且
成等比数列,且![]()
(Ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ) 设![]() 如果对任意正整数
如果对任意正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com