
 如图,过抛物线C1:y=x2-1上一点P(不与顶点重合)的切 线l与曲线C2:
如图,过抛物线C1:y=x2-1上一点P(不与顶点重合)的切 线l与曲线C2: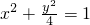 相交所得的弦为AB.
相交所得的弦为AB.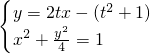 ,
,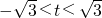 .
.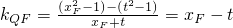 ,
, ,所以
,所以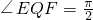 ,
, ,结论仍然成立.…(15分)
,结论仍然成立.…(15分)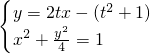 ,得4(1+t2)x2-4t(1+t2)x+(1-t2)(3+t2)=0.再由根的判别式和韦达定理能够证明弦AB的中点在一条定直线l0:y=-1上.
,得4(1+t2)x2-4t(1+t2)x+(1-t2)(3+t2)=0.再由根的判别式和韦达定理能够证明弦AB的中点在一条定直线l0:y=-1上.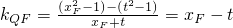 ,同理kQF=xE-t.所以kQF+kQE=(xE+xF)-2t=0.由此能够判断△EQF为直角三角形.
,同理kQF=xE-t.所以kQF+kQE=(xE+xF)-2t=0.由此能够判断△EQF为直角三角形.

科目:高中数学 来源: 题型:
 设椭圆C1:
设椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
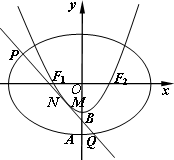
 (2010•潍坊三模)如图,过抛物线C1:y=x2-1上一点P(不与顶点重合)的切 线l与曲线C2:x2+
(2010•潍坊三模)如图,过抛物线C1:y=x2-1上一点P(不与顶点重合)的切 线l与曲线C2:x2+| y2 | 4 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练16练习卷(解析版) 题型:解答题
如图所示,抛物线C1:x2=4y,C2:x2=-2py(p>0).点M(x0,y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O).当x0=1-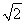 时,切线MA的斜率为-
时,切线MA的斜率为-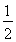 .
.
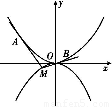
(1)求p的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
查看答案和解析>>
科目:高中数学 来源: 题型:
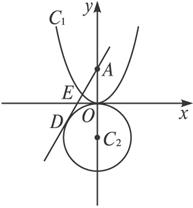
(1)证明(a+1)(y0+1)=1;
(2)若切线AD交抛物线C1于点E,且E为AD的中点,求点A纵坐标a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com