
| an |
| 2n |
| an |
| n+1 |
| 1 |
| bn |
| m |
| 20 |
| an |
| 2 |
| an-1 |
| 2n-1 |
| an |
| 2n |
| a1 |
| 21 |
| an |
| n+1 |
| (n+1)•2n |
| n+1 |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n |
| an |
| 2n |
| an-1 |
| 2n-1 |
| an |
| 2n |
| an |
| 2n |
| a1 |
| 21 |
| an |
| n+1 |
| (n+1)•2n |
| n+1 |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 3n |
| 1 |
| 3n+1 |
| 1 |
| 3n+2 |
| 1 |
| 3n+3 |
| 1 |
| 3n+1 |
| 1 |
| 3n+2 |
| 1 |
| 3n+3 |
| 1 |
| n+1 |
| 1 |
| 3n+1 |
| 1 |
| 3n+2 |
| 2 |
| 3n+3 |
| 1 |
| 3n+3 |
| 1 |
| 3n+3 |
| 2 |
| 3n+3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 19 |
| 20 |
| m |
| 20 |
| 19 |
| 20 |


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
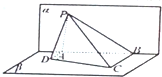 如图所示,△PAB所在的平面α和四边形AB所在的平面β互相垂直,AD⊥α,bc⊥α,AD=4,BC=8,AB=6,若tan∠ADP-2tan∠BCP=1,则动点P在平面内α的轨迹是( )
如图所示,△PAB所在的平面α和四边形AB所在的平面β互相垂直,AD⊥α,bc⊥α,AD=4,BC=8,AB=6,若tan∠ADP-2tan∠BCP=1,则动点P在平面内α的轨迹是( )| A、椭圆的一部分 |
| B、线段 |
| C、双曲线的一部分 |
| D、以上都不是 |
查看答案和解析>>
科目:高中数学 来源: 题型:
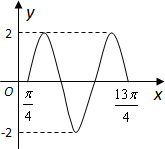 在研究性学习中,我校高三某班的一个课题研究小组做“关于横波的研究实验”.根据实验记载,他们观察到某一时刻的波形曲线符合函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=
在研究性学习中,我校高三某班的一个课题研究小组做“关于横波的研究实验”.根据实验记载,他们观察到某一时刻的波形曲线符合函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com