国家助学贷款是由财政贴息的信用贷款,旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2010届毕业生凌霄在本科期间共申请了24000元助学贷款,并承诺在毕业后3年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第13个月开始,每月工资比前一个月增加5%直到4000元.凌霄同学计划前12个月每个月还款额为500,第13个月开始,每月还款额比上一月多x元.
(Ⅰ)若凌霄恰好在第36个月(即毕业后三年)还清贷款,求x的值;
(Ⅱ)当x=50时,凌霄同学将在第几个月还清最后一笔贷款?他当月工资的余额是否能满足每月3000元的基本生活费?
(参考数据:1.0518=2.406,1.0519=2.526,1.0520=2.653,1.0521=2.786)
分析:方法一:(I)前12个月每月还款500,后24个月每月多x元,此36个数相加等于24000,得到x的一次方程,求出即可.
(II)设第n个月还清,前12个月每月还款500,后来(n-2)个月每月多还50,此n个数相加不小于24000,建立不等式解出n的范围.取最小 值.
方法二:(I)前12个月还款额是常数列,后二十四个月每月还款额构成一个等差数列,用数列公式求和,使和为24000,建立方程.解出每月应多还的数额.
(II)前12个月还款额是常数列,后n-12个月每月还款额构成一个首项为500,公差为50的等差数列,用数列公式求和,使和不小于24000,建立不等式,解出n的范围,取最小整数.
解答:解:(Ⅰ)依题意,从第13个月开始,
每月还款额比前一个月多x元,
故12×500+(500+x)+(500+2x)+…+(500+24x)=24000
即36×500+(1+2+3+…+24)x=24000,解得x=20(元).(6分)
即要使在三年全部还清,第13个月起每个月必须比上一个月多还20元.(7分)
(Ⅱ)设凌霄第n个月还清,
则应有12×500+(500+50)+(500+2×50)+…+[500+(n-12)×50]≥24000
即n
2-3n-828≥0,解之得
n≥>30,取n=31.(10分)
即凌霄工作31个月就可以还清贷款.
这个月凌霄的还款额为
24000-[12×500+(500+50)×(30-12)+•50]=450元(12分)
第31个月凌霄的工资为1500×1.05
19=1500×2.526=3789元.
因此,凌霄的剩余工资为3789-450=3339,
能够满足当月的基本生活需求.(14分)
解法2:(Ⅰ)依题意,从第13个月开始,
每个月的还款额为a
n构成等差数列,其中a
1=500+x,公差为x.(2分)
从而,到第36个月,凌霄共还款
12×500+24a1+•x(4分)
令
12×500+(500+x)×24+•x=24000,解之得x=20(元).(6分)
即要使在三年全部还清,第13个月起每个月必须比上一个月多还20元.(7分)
(Ⅱ)设凌霄第n个月还清,则应有
12×500+(500+50)×(n-12)+•50≥24000(8分)
整理可得n
2-3n-828≥0,解之得
n≥>30,取n=31.(10分)
即凌霄工作31个月就可以还清贷款.
这个月凌霄的还款额为
24000-[12×500+(500+50)×(30-12)+•50]=450元(12分)
第31个月凌霄的工资为1500×1.05
19=1500×2.526=3789元.
因此,凌霄的剩余工资为3789-450=3339,能够满足当月的基本生活需求.(14分)
点评:此为一可以转化为等差数列求和的问题,考查问题的转化能力,及等差数列求和公式的运用.



 元.
元. 值;(6分)
值;(6分) 时,凌霄同学将在毕业后第几个月还清最后一笔贷款?他当月工资余额能否满足当月3000元的基本生活费?(6分)
时,凌霄同学将在毕业后第几个月还清最后一笔贷款?他当月工资余额能否满足当月3000元的基本生活费?(6分)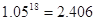 ,
, ,
,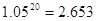 ,
,  )
)