练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，在平行四边形ABCD中，AE：EB=1：2，若S△AEF=6cm2 ， 则S△ADF为（　　）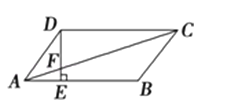

    A.54cm2
    B.24cm2
    C.18cm2
    D.12cm2

    【答案】C
    【解析】解：∵AE∥CD，∴△AEF∽△CDF，
    ∴AE：CD=AF：CF，
    ∵AE：EB=1：2，
    ∴AE：AB=AE：CD=1：3，
    ∴AF：CF=1：3，
    ∴AF：AC=1：4，
    ∴△AEF与△ABC的高的比为1：4，
    ∴△AEF与△ABC的面积的比为1：12，
    ∴△AEF与平行四边形ABCD的面积的比为1：24，
    ∵△AEF的面积等于6cm2 ，
    ∴平行四边形ABCD的面积等于144cm2 ．
    ∵AF：AC=1：4，
    ∴S△ADF=18cm2 ．
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知 =（cosα，sinα）， =（cosβ，sinβ），其中0＜α＜β＜π．
    （1）求证： 与 互相垂直；
    （2）若k 与 ﹣k 的长度相等，求β﹣α的值（k为非零的常数）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果将函数f（x）=sin（3x+φ）（﹣π＜φ＜0）的图象向左平移 个单位所得到的图象关于原点对称，那么φ=

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】当|a|≤1，|x|≤1时，关于x的不等式|x2﹣ax﹣a2|≤m恒成立，则实数m的取值范围是（　　）
    A.[ ， +∞）
    B.[ ， +∞）
    C.[ ， +∞）
    D.[ ， +∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x﹣1|+|x﹣a|
    （1）当a=2时，解不等式f（x）≥4．
    （2）若不等式f（x）≥2a恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AB是圆O的直径，PB是圆O的切线，过A点作AE∥OP交圆O于E点，PA交圆O于点F，连接PE．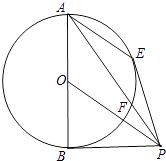

    （1）求证：PE是圆O的切线；
    （2）设AO=3，PB=4，求PF的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应：

    X

    2

    4

    5

    6

    8

    y

    30

    40

    60

    50

    70


    （1）求回归直线方程．
    （2）回归直线必经过的一点是哪一点？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三点O（0，0），A（﹣2，1），B（2，1），曲线C上任意一点M（x，y）满足| + |= （ + ）+2．
    （1）求曲线C的方程；
    （2）动点Q（x0 ， y0）（﹣2＜x0＜2）在曲线C上，曲线C在点Q处的切线为直线l：是否存在定点P（0，t）（t＜0），使得l与PA，PB都相交，交点分别为D，E，且△QAB与△PDE的面积之比是常数？若存在，求t的值．若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}的前n项和为Sn ， 则下列不可能成立的（ ）
    A.a2016（S2016﹣S2015）=0
    B.a2016（S2016﹣S2014）=0
    C.（a2016﹣a2013）（S2016﹣S2013）=0
    D.（a2016﹣a2012）（S2016﹣S2012）=0

    查看答案和解析>>

    同步练习册答案