
某工厂建一个长方形无盖蓄水池,其容积为4800m3,深度为3m。如果池底每1 m2的造价为150元,池壁每1 m2的造价为120元,怎么设计水池能使造价最低?最低造价多少元?
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由形状为长方形A1B1C1D1的休闲区和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米(如图所示).
(1)若设休闲区的长和宽的比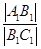 =x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
=x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,则休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
图1是某斜拉式大桥图片,为了了解桥的一些结构情况,学校数学兴趣小组将大桥的结构进行了简化,取其部分可抽象成图2所示的模型,其中桥塔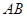 、
、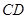 与桥面
与桥面 垂直,通过测量得知
垂直,通过测量得知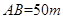 ,
,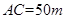 ,当
,当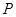 为
为 中点时,
中点时,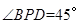 .
.
(1)求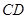 的长;
的长;
(2)试问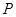 在线段
在线段 的何处时,
的何处时,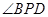 达到最大.
达到最大.
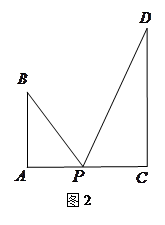
|
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知△ABC的顶点A(3,0),B(0,1),C(1,1),P(x,y)在△ABC内部(包括边界),若目标函数z= (a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
(a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com