
如图,四棱锥S—ABCD的底面为正方形,SD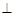 底面ABCD,则下列结论中不正确的是
底面ABCD,则下列结论中不正确的是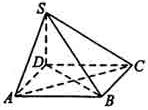
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D.AB与SC所成的角等于DC与SA所成的角 |
D
解析试题分析:设BD、AC相较于点O,
因为SD⊥底面ABCD,底面ABCD为正方形,所以连接BD,则BD⊥AC,根据三垂线定理,可得AC⊥SB,故A正确;
因为AB∥CD,AB?平面SCD,CD?平面SCD,所以AB∥平面SCD,故B正确;
因为SD⊥底面ABCD,∠ASO是SA与平面SBD所成的角,∠DSO是SC与平面SBD所成的,而△SAO≌△CSO,所以∠ASO=∠CSO,即SA与平面SBD所成的角等于SC与平面SBD所成的角,故C正确;
∵AB∥CD,∴AB与SC所成的角是∠SCD,DC与SA所成的角是∠SAB,而这两个角显然不相等,故D不正确;故选D.
考点:线面垂直的判定定理;线面垂直的性质定理;线面平行的判断定理;线面角;异面直线所成的角。
点评:此题考查的知识点较多,综合性强,是个中档题.做本题的关键是熟练掌握线面垂直的性质定理和线面平行的判定定理,以及直线与平面所成的角,异面直线所成的角等问题,.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:单选题
(文)如图,在棱长为4的正方体ABCD—A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′?上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( )
A. B. C. D.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
一个盛满水的三棱锥容器,如图所示,不久发现三个侧棱上各有一个小洞D,E,F。且知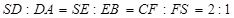 ,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )
,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )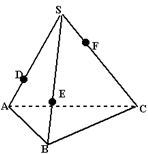
A.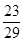 | B.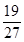 | C.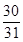 | D.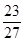 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
把正方形ABCD沿对角线AC折起,当以A、B、C、D四点为顶点的棱锥体积最大时,直线BD和平面ABC所成的角的大小为 ( )
A. 90° B .60° C . 45° D .30°
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设四棱锥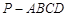 的底面不是平行四边形,用平面
的底面不是平行四边形,用平面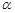 去截此四棱锥,使得截面是平行四边形,则这样的平面
去截此四棱锥,使得截面是平行四边形,则这样的平面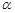 ( )
( )
| A.不存在 | B.有且只有1个 | C.恰好有4个 | D.有无数多个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com