
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线经过点(0,1),求实数
处的切线经过点(0,1),求实数![]() 的值;
的值;
(Ⅱ)求证:当![]() 时,函数
时,函数![]() 至多有一个极值点;
至多有一个极值点;
 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 在
在![]() 上且
上且![]() .
.
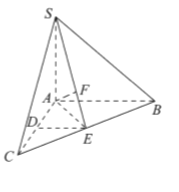
(I)求证:![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(III)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】英语老师要求学生从星期一到星期四每天学习3个英语单词:每周五对一周内所学单词随机抽取若干个进行检测(一周所学的单词每个被抽到的可能性相同)
(1)英语老师随机抽了![]() 个单词进行检测,求至少有
个单词进行检测,求至少有![]() 个是后两天学习过的单词的概率;
个是后两天学习过的单词的概率;
(2)某学生对后两天所学过的单词每个能默写对的概率为![]() ,对前两天所学过的单词每个能默写对的概率为
,对前两天所学过的单词每个能默写对的概率为![]() ,若老师从后三天所学单词中各抽取一个进行检测,求该学生能默写对的单词的个数
,若老师从后三天所学单词中各抽取一个进行检测,求该学生能默写对的单词的个数![]() 的分布列和期望。
的分布列和期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,M是PD的中点.

(Ⅰ)求证:OM∥平面PAB;
(Ⅱ)平面PBD⊥平面PAC;
(Ⅲ)当三棱锥C﹣PBD的体积等于 ![]() 时,求PA的长.
时,求PA的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于顶点在原点的抛物线,给出下列条件:
①焦点在y轴上;
②焦点在x轴上
③抛物线上横坐标为1的点到焦点的距离等于6;
④抛物线的过焦点且垂直于对称轴的弦的长为5;
⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1)
能使抛物线方程为y2=10x的条件是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美国制裁中兴,未来7年一颗芯片都不卖,这却激发了中国“芯”的研究热潮.某公司甲,乙,丙三个研发小组分别研发![]() ,
,![]() ,
,![]() 三种不同的芯片,现在用分层抽样的方法从这些芯片中抽取若干件进行质量分析,有关数据见下表(单位:件).
三种不同的芯片,现在用分层抽样的方法从这些芯片中抽取若干件进行质量分析,有关数据见下表(单位:件).
芯片 | 数量 | 抽取件数 |
| 200 |
|
| 600 |
|
| 400 | 2 |
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若在这抽出的样品中随机抽取2件送往某机构进行进一步检测,求这2件芯片来自不同种类的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆中心为坐标原点O,对称轴为坐标轴,且过M(2, ![]() ) ,N(
) ,N(![]() ,1)两点,
,1)两点,
(I)求椭圆的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆C恒有两个交点A,B,且![]() ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com