
【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.05 |
第2组 | [60,70) |
| 0.35 |
第3组 | [70,80) | 30 |
|
第4组 | [80,90) | 20 | 0.20 |
第5组 | [90,100] | 10 | 0.10 |
合计 | 100 | 1.00 |
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率。
【答案】(1) 35,0.30;(2)![]() .
.
【解析】
试题(Ⅰ)直接利用频率和等于1求出b,用样本容量乘以频率求a的值;
(Ⅱ)由分层抽样方法求出所抽取的6人中第三、第四、第五组的学生数,利用列举法写出从中任意抽取2人的所有方法种数,查出2人至少1人来自第四组的事件个数,然后利用古典概型的概率计算公式求解.
试题解析:
(Ⅰ)a=100-5-30-20-10=35,b=1-0.05-0.35-0.20-0.10=0.30
(Ⅱ )因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,
每组分别为,第3组:![]() ×30=3人,第4组:
×30=3人,第4组:![]() ×20=2人,第5组:
×20=2人,第5组:![]() ×10=1人,
×10=1人,
所以第3、4、5组应分别抽取3人、2人、1人
设第3组的3位同学为A1、A2、A3,第4组的2位同学为B1、B2,第5组的1位同学为C1,则从6位同学中抽2位同学有15种可能,如下:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1).其中第4组被入选的有9种,
所以其中第4组的2位同学至少有1位同学入选的概率为![]() =
=![]()


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() 两点
两点
(1) 求![]() 的直角坐标方程和
的直角坐标方程和![]() 的普通方程;
的普通方程;
(2) 若![]() ,
,![]() ,
,![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·新课标1卷)已知椭圆E的中心为坐标原点,离心率为![]() , E的右焦点与抛物线C:y2=8x的焦点重合,A,B是C的准线与E的两个交点,则|AB|= ( )
, E的右焦点与抛物线C:y2=8x的焦点重合,A,B是C的准线与E的两个交点,则|AB|= ( )
A.3
B.6
C.9
D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装店为庆祝开业“三周年”,举行为期六天的促销活动,规定消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,第五天该服装店经理对前五天中参加抽奖活动的人数进行统计,![]() 表示第
表示第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 |
| 4 | 6 | 10 | 23 | 22 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)预测第六天的参加抽奖活动的人数(按四舍五入取到整数).
参考公式与参考数据: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市出租车的计价标准是:4km以内(含4km)10元,超过4km且不超过18km的部分1.2元/km,超过18km的部分1.8元/km,不计等待时间的费用.
(1)如果某人乘车行驶了10km,他要付多少车费?
(2)试建立车费y(元)与行车里程x(km)的函数关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P - ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC![]()
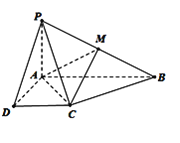
(1)证明平面PAD⊥平面PCD;
(2)求AC与PB所成角的余弦值;
(3)求平面AMC与平面BMC所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年五一小长假,以洪崖洞、李子坝轻轨、长江索道、一棵树观景台为代表的网红景点,把重庆推上全国旅游人气搒的新高.外地客人小胖准备游览上面这![]() 个景点,他游览每一个景台的概率都是
个景点,他游览每一个景台的概率都是![]() ,且他是否游览哪个景点互不影响.设
,且他是否游览哪个景点互不影响.设![]() 表示小胖离开重庆时游览的景点数与没有游览的景点数之差的绝对值.
表示小胖离开重庆时游览的景点数与没有游览的景点数之差的绝对值.
(1)记“函数![]() 是实数集
是实数集![]() 上的偶函数”为事件
上的偶函数”为事件![]() ,求事件
,求事件![]() 的概率.
的概率.
(2)求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=logm![]() (m>0且m≠1),
(m>0且m≠1),
(I)判断f(x)的奇偶性并证明;
(II)若m=![]() ,判断f(x)在(3,+∞)的单调性(不用证明);
,判断f(x)在(3,+∞)的单调性(不用证明);
(III)若0<m<1,是否存在β>α>0,使f(x)在[α,β]的值域为[logmm(β-1),logm(α-1)]?若存在,求出此时m的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com