
【题目】已知函数f(x)= ![]() 若f(2﹣a2)>f(a),则实数a的取值范围为 .
若f(2﹣a2)>f(a),则实数a的取值范围为 .
【答案】(﹣2,1)
【解析】解:函数f(x),当x≥0 时,f(x)=x2+4x,由二次函数的性质知,它在[0,+∞)上是增函数,
当x<0时,f(x)=4x﹣x2,由二次函数的性质知,它在(﹣∞,0)上是增函数,
该函数连续,则函数f(x) 是定义在R 上的增函数
∵f(2﹣a2)>f(a),
∴2﹣a2>a
解得﹣2<a<1
实数a 的取值范围是(﹣2,1)
所以答案是:(﹣2,1)
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() ,点P(4,0),过右焦点F作与y轴不垂直的直线l交椭圆C于A,B两点. (Ⅰ)求椭圆C的离心率;
,点P(4,0),过右焦点F作与y轴不垂直的直线l交椭圆C于A,B两点. (Ⅰ)求椭圆C的离心率;
(Ⅱ)求证:以坐标原点O为圆心与PA相切的圆,必与直线PB相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() (b≠0).
(b≠0).
(1)若函数f(x)在定义域上是单调函数,求实数b的取值范围;
(2)求函数f(x)的极值点;
(3)令b=1, ![]() ,设A(x1 , y1),B(x2 , y2),C(x3 , y3)是曲线y=g(x)上相异三点,其中﹣1<x1<x2<x3 . 求证:
,设A(x1 , y1),B(x2 , y2),C(x3 , y3)是曲线y=g(x)上相异三点,其中﹣1<x1<x2<x3 . 求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”“生二孩能休多久产假”等成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查,得到如下数据:
产假安排(单位:周) | 14 | 15 | 16 | 17 | 18 |
有生育意愿家庭数 | 4 | 8 | 16 | 20 | 26 |
(1)若用表中数据所得的频率代替概率,面对产假为14周与16周,估计某家庭有生育意愿的概率分别为多少?
(2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择.
①求两种安排方案休假周数和不低于32周的概率;
②如果用ξ表示两种方案休假周数和.求随机变量ξ的分布及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且f(x+2)=f(x)对x∈R恒成立,当x∈[0,1]时,f(x)=2x , 则f(﹣log224)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|y= ![]() },集合B={x|y=lg(﹣x2﹣7x﹣12)},集合C={x|m+1≤x≤2m﹣1}.
},集合B={x|y=lg(﹣x2﹣7x﹣12)},集合C={x|m+1≤x≤2m﹣1}.
(1)求A∩B;
(2)若A∪C=A,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且cos2B+3cos(A+C)+2=0, ![]() ,那么△ABC周长的最大值是( )
,那么△ABC周长的最大值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)与g(x)的图象关于原点对称,且它们的图象拼成如图所示的“Z”形折线段ABOCD,不含A(0,1),B(1,1),O(0,0),C(﹣1,﹣1),D(0,﹣1)五个点.则满足题意的函数f(x)的一个解析式为 . 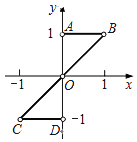
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com