
【题目】千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区A的100天日落和夜晚天气,得到如下![]() 列联表:
列联表:
夜晚天气 日落云里走 | 下雨 | 未下雨 |
出现 | 25 | 5 |
未出现 | 25 | 45 |
临界值表 | ||||
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
并计算得到![]() ,下列小波对地区A天气判断不正确的是( )
,下列小波对地区A天气判断不正确的是( )
A.夜晚下雨的概率约为![]()
B.未出现“日落云里走”夜晚下雨的概率约为![]()
C.有![]() 的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
D.出现“日落云里走”,有![]() 的把握认为夜晚会下雨
的把握认为夜晚会下雨
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某市组织高三全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如下:
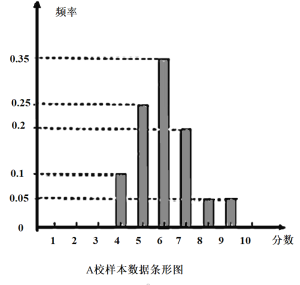
B校样本数据统计表:
成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
(1)计算两校样本数据的均值和方差,并根据所得数据进行比较.
(2)从A校样本数据成绩分别为7分、8分和9分的学生中按分层抽样方法抽取6人,若从抽取的6人中任选2人参加更高一级的比赛,求这2人成绩之和大于或等于15的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (
(![]() )的离心率为
)的离心率为![]() ,F是E的右焦点,过点F的直线交E于点
,F是E的右焦点,过点F的直线交E于点![]() 和点
和点![]() (
(![]() ).当直线
).当直线![]() 与x轴垂直时,
与x轴垂直时,![]() .
.
(1)求椭圆E的方程;
(2)设直线l:![]() 交x轴于点G,过点B作x轴的平行线交直线l于点C.求证:直线
交x轴于点G,过点B作x轴的平行线交直线l于点C.求证:直线![]() 过线段
过线段![]() 的中点.
的中点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂![]() ,
,![]() 两条相互独立的生产线生产同款产品,在产量一样的情况下,通过日常监控得知,
两条相互独立的生产线生产同款产品,在产量一样的情况下,通过日常监控得知,![]() ,
,![]() 生产线生产的产品为合格品的概率分别为
生产线生产的产品为合格品的概率分别为![]() 和
和![]() .
.
(1)从![]() ,
,![]() 生产线上各抽检一件产品,若使得产品至少有一件合格的概率不低于99.5%,求
生产线上各抽检一件产品,若使得产品至少有一件合格的概率不低于99.5%,求![]() 的最小值
的最小值![]() ;
;
(2)假设不合格的产品均可进行返工修复为合格品,以(1)中确定的![]() 作为
作为![]() 的值.
的值.
①已知![]() ,
,![]() 生产线的不合格品返工后每件产品可分别挽回损失5元和3元,若从两条生产线上各随机抽检1000件产品,以挽回损失的平均数为判断依据,估计哪条生产线的挽回损失较多?
生产线的不合格品返工后每件产品可分别挽回损失5元和3元,若从两条生产线上各随机抽检1000件产品,以挽回损失的平均数为判断依据,估计哪条生产线的挽回损失较多?
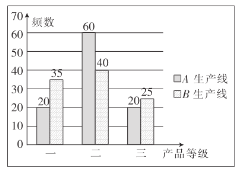
②若最终的合格品(包括返工修复后的合格品)按照一、二、三等级分类后,每件可分别获利10元、8元、6元,现从![]() ,
,![]() 生产线的最终合格品中各随机抽取100件进行分级检测,结果统计如图所示,用样本的频率分布估计总体分布,记该工厂生产一件产品的利润为
生产线的最终合格品中各随机抽取100件进行分级检测,结果统计如图所示,用样本的频率分布估计总体分布,记该工厂生产一件产品的利润为![]() ,求
,求![]() 的分布列并估计该厂产量2000件时利润的期望值.
的分布列并估计该厂产量2000件时利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为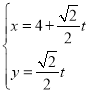 (t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cos θ,直线l与圆C交于A,B两点.
(t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cos θ,直线l与圆C交于A,B两点.
(1)求圆C的直角坐标方程及弦AB的长;
(2)动点P在圆C上(不与A,B重合),试求△ABP的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com