
【题目】一条光线从点(﹣2,﹣3)射出,经y轴反射后与圆(x+3)2+(y﹣2)2=1相切,则反射光线所在直线的斜率为( )
A.﹣ ![]() 或﹣
或﹣ ![]()
B.﹣ ![]() 或﹣
或﹣ ![]()
C.﹣ ![]() 或﹣
或﹣ ![]()
D.﹣ ![]() 或﹣
或﹣ ![]()
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() )的图象,只需将函数y=sin2x的图象上所有的点( )
)的图象,只需将函数y=sin2x的图象上所有的点( )
A.向左平移 ![]() 个单位
个单位
B.向左平移 ![]() 个单位
个单位
C.向右平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某中草药材的销售量与年份有关,下表是近五年的部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
销售量(吨) | 114 | 115 | 116 | 116 | 114 |
(1)利用所给数据求年销售量![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)利用(1)中所求出的直线方程预测该地2018年的中草药的销售量.
参考公式: 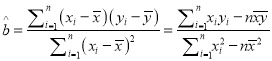 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=log2( ![]() +a).
+a).
(1)当a=5时,解不等式f(x)>0;
(2)若关于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,求a的取值范围.
(3)设a>0,若对任意t∈[ ![]() ,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在直线y=4x上,且与直线l:x+y﹣2=0相切于点P(1,1)
(Ⅰ)求圆的方程
(II)直线kx﹣y+3=0与该圆相交于A、B两点,若点M在圆上,且有向量 ![]() (O为坐标原点),求实数k.
(O为坐标原点),求实数k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知三点A(-1,0)、B(t,2)、C(2,1),t∈R,O为坐标原点
(I)若△ABC是∠B为直角的直角三角形,求t的值
(Ⅱ)若四边形ABCD是平行四边形,求![]() 的最小值
的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
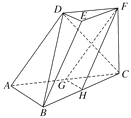
【题目】如图,三棱台DEF ABC中,AB=2DE,G,H分别为AC,BC的中点.
(1)求证:平面ABED∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com