
在 中,角
中,角 、
、 、
、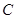 的对边分别为
的对边分别为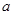 、
、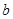 、
、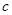 .设向量
.设向量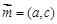 ,
,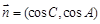 .
.
(1)若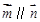 ,
,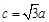 ,求角
,求角 ;(2)若
;(2)若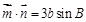 ,
,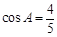 ,求
,求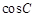 的值.
的值.
(1)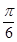 (2)
(2)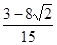
解析试题分析:(1)解三角形,一般利用正余弦定理,将等量关系统一成角或边.首先由向量平行坐标关系得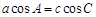 再根据正弦定理或余弦定理,将等式化为
再根据正弦定理或余弦定理,将等式化为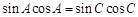 或
或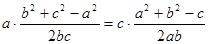 ,结合三角形中角的限制条件,得
,结合三角形中角的限制条件,得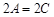 或
或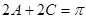 ,或利用因式分解化为
,或利用因式分解化为 ,从而有
,从而有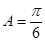 ,(2)由向量数量积坐标关系得
,(2)由向量数量积坐标关系得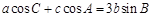 再根据正弦定理或余弦定理,将等式化为
再根据正弦定理或余弦定理,将等式化为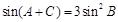 或
或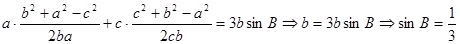 ,再由两角和余弦公式求出
,再由两角和余弦公式求出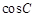 的值.
的值.
试题解析:(1)∵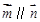 ,∴
,∴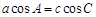 .由正弦定理,得
.由正弦定理,得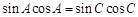 .
.
化简,得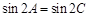 .… 2分∵
.… 2分∵ ,∴
,∴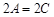 或
或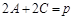 ,从而
,从而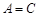 (舍)或
(舍)或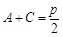 .∴
.∴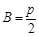 .… 4分 在Rt△ABC中,
.… 4分 在Rt△ABC中,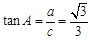 ,
,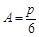 .…6分
.…6分
(2)∵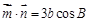 ,∴
,∴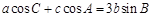 .
.
由正弦定理,得 ,从而
,从而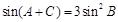 .
.
∵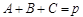 ,∴
,∴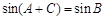 . 从而
. 从而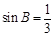 . 8分
. 8分
∵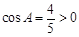 ,
,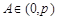 ,∴
,∴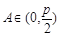 ,
,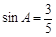 . 10分
. 10分
∵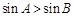 ,∴
,∴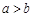 ,从而
,从而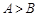 ,B为锐角,
,B为锐角,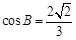 . 12分
. 12分
∴ =
=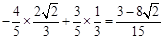 . 14分
. 14分
考点:正余弦定理, 两角和余弦公式


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
在海岸A处,发现北偏东45°方向、距离A处( -1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10
-1)海里的B处有一艘走私船;在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10 海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
海里/小时的速度追截走私船.同时,走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?最少要花多少时间?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,内角A,B,C所对的边分别是a,b,c.已知bsin A=3csin B,a=3,cos B=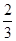
(1)求b的值;
(2)求sin 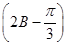 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com