
给出四个函数,分别满足①f(x+y)=f(x)+f(y),②g(x+y)=g(x)·g(y),③h(x·y)=h(x)+h(y),④m(x·y)=m(x)·m(y).又给出四个函数的图像,那么正确的匹配方案可以是 ( )




甲 乙 丙 丁
A.①甲,②乙,③丙,④丁 B.①乙,②丙,③甲,④丁
C.①丙,②甲,③乙,④丁 D.①丁,②甲,③乙,④丙
D
【解析】
试题分析::①f(x)=x,这个函数可使 f(x+y)=x+y=f(x)+f(y)成立,
∵f(x+y)=x+y,x+y=f(x)+f(y),∴f(x+y)=f(x)+f(y),自变量的和等于因变量的和.
正比例函数y=kx就有这个特点.故①-丁;②寻找一类函数g(x),使得g(x+y)=g(x)g(y),即自变量相加等于因变量乘积.指数函数y=ax(a>0,a≠1)具有这种性质:g(x)=ax,g(y)=ay,g(x+y)=ax+y=ax•ay=g(x)•g(y).故②-甲;③自变量的乘积等于因变量的和:与②相反,可知对数函数具有这种性质:
令:h(x)=logax,则h(xy)=loga(xy)=logax+logbx.故③-乙.④t(x)=x2,这个函数可使t(xy)=t(x)t(y)成立.∵t(x)=x2,∴t(xy)=(xy)2=x2y2=t(x)t(y),故④-丙.故选D.
考点:1.对数函数、指数函数的图像与性质;2.一次函数的性质与图象.


科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省高三上学期第三次考试文科数学卷 题型:选择题
1.
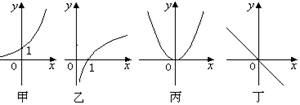
给出四个函数,分别满足:
① ;②
;②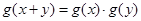 ;③
;③ ;
;
④ 。又给出四个函数的图象,则正确的匹配方案是( )
。又给出四个函数的图象,则正确的匹配方案是( )
A.①-甲,②-乙,③-丙,④-丁 ;
B.①-乙,②-丙,③-丁,④-甲;
C.①-丙,②-甲,③-乙,④-丁 ; www..com
D.①-丁,②-甲,③-乙,④-丙。
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二上学期期中理科数学试卷 题型:选择题
给出四个函数,分别满足①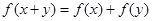 ;②
;② ;
;
③ ;④
;④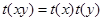 ,又给出四个函数图象
,又给出四个函数图象

正确的匹配方案是 ( * )
A. ①—丁 ②—乙 ③—丙 ④—甲
B. ①—乙 ②—丙 ③—甲 ④—丁
C. ①—丙 ②—甲 ③—乙 ④—丁
D. ①—丁 ②—甲 ③—乙 ④—丙
查看答案和解析>>
科目:高中数学 来源:河北省正定中学2010届高三上学期第一次月考(理) 题型:选择题
给出四个函数,分别满足:①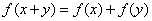 ②
②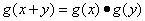
③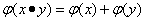 ④
④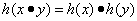 又给出四个函数的图像,则正确的匹配方案是( )
又给出四个函数的图像,则正确的匹配方案是( )
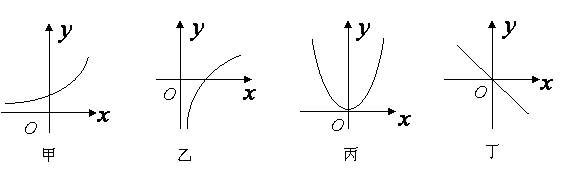
A.①-甲,②-乙,③-丙,④-丁 B.①-乙,②-丙,③-丁,④-甲
C.①-丙,②-甲,③-乙,④-丁 D.①-丁,②-甲,③-乙,④-丙
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com