
 在区间[1,4]上有不动点,求常数a的取值范围.
在区间[1,4]上有不动点,求常数a的取值范围. ,讨论将a分离出来,利用导数研究出等式另一侧函数的取值范围即可求出a的范围.
,讨论将a分离出来,利用导数研究出等式另一侧函数的取值范围即可求出a的范围.
 (6分);
(6分); (8分),
(8分), (9分),
(9分), (
( ,舍去)(10分),
,舍去)(10分),| x | (1,2) | 2 | (2,4) |
| a′ | + | - | |
| a | ↗ | 最大值 | ↘ |
 (13分),
(13分), (14分).
(14分).

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源: 题型:
| 5 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
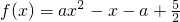 在区间[1,4]上有不动点,求常数a的取值范围.
在区间[1,4]上有不动点,求常数a的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省江门市新会一中高三(上)第三次检测数学试卷(文科)(解析版) 题型:填空题
 在区间[1,4]上存在次不动点,则实数a的取值范围是 .
在区间[1,4]上存在次不动点,则实数a的取值范围是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com