
【题目】已知数列![]() 中,
中,![]() ,点
,点![]() (
(![]() )在直线y = x上,
)在直线y = x上,
(Ⅰ)计算a2,a3,a4的值;
(Ⅱ)令bn=an+1﹣an﹣1,求证:数列{bn}是等比数列;
(Ⅲ)设Sn、Tn分别为数列{an}、{bn}的前n项和,是否存在实数λ,使得数列![]() 为等差数列?若存在,试求出λ的值;若不存在,请说明理由.
为等差数列?若存在,试求出λ的值;若不存在,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析;(Ⅲ)存在λ=2.
;(Ⅱ)见解析;(Ⅲ)存在λ=2.
【解析】试题分析:(1)根据点![]() 在直线
在直线![]() 上,可得
上,可得![]() ,代入计算可得
,代入计算可得![]() 的值;(2)利用
的值;(2)利用![]() ,及
,及![]() ,即可证明数列
,即可证明数列![]() 是等比数列;(3)求得数列的前三项,求得
是等比数列;(3)求得数列的前三项,求得![]() ,再验证即可求得结论.
,再验证即可求得结论.![]()
试题解析:(Ⅰ)由题意,∵点(n,2an+1﹣an)在直线y=x上,
∴2an+1﹣an=n
∵![]() ,∴
,∴![]() ,
,
同理,![]() ,
,![]() ;
;
(Ⅱ)证明:∵bn=an+1﹣an﹣1,2an+1﹣an=n
∴bn+1=an+2﹣an+1﹣1=![]() ﹣an+1﹣1=
﹣an+1﹣1=![]() (an+1﹣an﹣1)=
(an+1﹣an﹣1)=![]() bn,
bn,
∵b1=a2﹣a1﹣1=﹣![]()
∴数列{bn}是以﹣![]() 为首项,
为首项,![]() 为公比的等比数列;
为公比的等比数列;
(Ⅲ)解:存在λ=2,使数列![]() 是等差数列.
是等差数列.
由(Ⅱ)知,![]() ,
,![]() ,
,
∵an+1=n﹣1﹣bn=n﹣1+![]() ,∴an=n﹣2+
,∴an=n﹣2+![]() ,
,
∴Sn= =
=![]()
由题意,要使数列![]() 是等差数列,则
是等差数列,则![]()
∴2×![]() =
=![]() ﹣
﹣![]() λ+
λ+![]() ,∴λ=2
,∴λ=2
当λ=2时,![]() =
=![]() ,数列是等差数列
,数列是等差数列
∴当且仅当λ=2时,数列是等差数列.


科目:高中数学 来源: 题型:
【题目】某企业准备投入适当的广告费对产品进行促销,在一年内预计销售量Q(万件)与广告费x(万元)之间的函数关系为Q=![]() (x>1),已知生产该产品的年固定投入为3万元,每生产1万件该产品另需再投入32万元,若每件销售价为“年平均每件生产成本(生产成本不含广告费)的150%”与“年平均每件所占广告费的50%”之和.
(x>1),已知生产该产品的年固定投入为3万元,每生产1万件该产品另需再投入32万元,若每件销售价为“年平均每件生产成本(生产成本不含广告费)的150%”与“年平均每件所占广告费的50%”之和.
(1)试将年利润W(万元)表示为年广告费x(万元)的函数;(年利润=销售收入-成本)
(2)当年广告费为多少万元时,企业的年利润最大?最大年利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲,乙两种产品均需用![]() 两种原料,已知生产1吨每种产品需用
两种原料,已知生产1吨每种产品需用![]() 原料及每天原料的可用限额如下表所示,如果生产1吨甲,乙产品可获利润分别为3万元、4万元,则该企业可获得最大利润为__________万元.
原料及每天原料的可用限额如下表所示,如果生产1吨甲,乙产品可获利润分别为3万元、4万元,则该企业可获得最大利润为__________万元.
甲 | 乙 | 原料限额 | |
A(吨) | 3 | 2 | 12 |
B(吨) | 1 | 2 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是直线
是直线![]() 与椭圆
与椭圆![]() 的一个公共点,
的一个公共点,![]() 分别为该椭圆的左右焦点,设
分别为该椭圆的左右焦点,设![]() 取得最小值时椭圆为
取得最小值时椭圆为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)已知![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的两点,
轴对称的两点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,试判断
,试判断![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为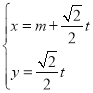 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为![]() (单位:
(单位:![]() ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为![]() (单位:元)
(单位:元)

(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com