
【题目】在平面直角坐标系xOy中,已知直线y=﹣2x+1与圆O:x2+y2=r2(r>0)交于M,N两点,且MN=![]() .
.
(1)求M,N的坐标;
(2)求过O,M,N三点的圆的方程.
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】设f(x)=2 ![]() sin(π﹣x)sinx﹣(sinx﹣cosx)2 .
sin(π﹣x)sinx﹣(sinx﹣cosx)2 .
(1)求f(x)的单调递增区间;
(2)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移 ![]() 个单位,得到函数y=g(x)的图象,求g(
个单位,得到函数y=g(x)的图象,求g( ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司咪推广线下分店,计划在![]() 市的
市的![]() 区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记
区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记![]() 表示在各区开设分店的个数,
表示在各区开设分店的个数, ![]() 表示这个
表示这个![]() 个分店的年收入之和.
个分店的年收入之和.
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)假设该公司在![]() 区获得的总年利润
区获得的总年利润![]() (单位:百万元)与
(单位:百万元)与![]() 之间的关系为
之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在
,请结合(1)中的线性回归方程,估算该公司应在![]() 区开设多少个分店时,才能使
区开设多少个分店时,才能使![]() 区平均每个店的年利润最大?
区平均每个店的年利润最大?
(参考公式: ![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆![]() 离心率是
离心率是![]() ,焦点到相应准线的距离是3.
,焦点到相应准线的距离是3.
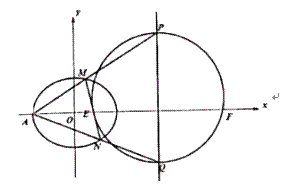
(1)求椭圆的方程;
(2)如图,设A是椭圆的左顶点,动圆过定点E(1,0)和F(7,0),且与直线x=4交于点P,Q.
①求证:AP,AQ斜率的积是定值;
②设AP,AQ分别与椭圆交于点M,N,求证:直线MN过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,抛物线![]() 的焦点为
的焦点为![]() .
.
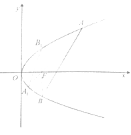
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过![]() 的两条直线分别与抛物线
的两条直线分别与抛物线![]() 交于点
交于点![]() ,
,![]() 与
与![]() ,
,![]() (点
(点![]() ,
,![]() 在
在![]() 轴的上方).
轴的上方).
①若![]() ,求直线
,求直线![]() 的斜率;
的斜率;
②设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,若
,若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类比三角形中的性质:(1)两边之和大于第三边;(2)中位线长等于底边的一半;(3)三内角平分线交于一点; 可得四面体的对应性质:(1)任意三个面的面积之和大于第四个面的面积;(2)过四面体的交于同一顶点的三条棱的中点的平面面积等于第四个面面积的![]() ;(3)四面体的六个二面角的平分面交于一点。其中类比推理结论正确的有 ( )
;(3)四面体的六个二面角的平分面交于一点。其中类比推理结论正确的有 ( )
A. (1) B. (1)(2) C. (1)(2)(3) D. 都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com