
分析 (Ⅰ)设二次函数f(x)=ax2+bx+c(a≠0),由已知构造方程组求出a,b,c值,可得函数f(x)的解析式;
(Ⅱ) 由(I)得:g(x)=f(x)-3x-6=x2-4x-5,则y=g(log3x)=${(lo{g}_{3}x-2)}^{2}-9$,进而可得区间$[\frac{1}{9},27]$上函数的最值和最值点.
解答 解:(Ⅰ)由已知设二次函数f(x)=ax2+bx+c(a≠0),
由f(0)=1可得c=1,
从而:y=f(x)-x-4=ax2+bx+1-x-4=ax2+(b-1)x-3
∵-1和3是函数y=f(x)-x-4的两个零点,
∴由韦达定理可得$\left\{\begin{array}{l}-\frac{b-1}{a}=-1+3=2\\-\frac{3}{a}=-1×3=-3\end{array}\right.$,解得$\left\{\begin{array}{l}a=1\\ b=-1\end{array}\right.$
故f(x)的解析式为f(x)=x2-x+1
(Ⅱ)由题设及(Ⅰ)得g(x)=(x2-x+1)-3x-6=x2-4x-5
从而:$y=g({log_3}x)={log_3}^2x-4{log_3}x-5={({log_3}x-2)^2}-9$∵$\frac{1}{9}≤x≤27$,
∴-2≤log3x≤3故:当log3x=2时,即x=9时,ymin=-9;
当log3x=-2时,即$x=\frac{1}{9}$时,ymax=7.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在区间$(0,\frac{2}{3}π)$上单调递增 | |
| B. | 直线$x=\frac{π}{8}$是函数y=f(x)图象的一条对称轴 | |
| C. | 点$(\frac{π}{4},0)$是函数y=f(x)图象的一个对称中心 | |
| D. | 将函数y=f(x)的图象向左平移$\frac{π}{8}$个单位,可得到$y=\sqrt{2}sin2x$的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{11}{6}$ | C. | $\frac{11}{3}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
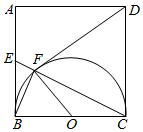 如图,正方形ABCD中,E是AB的中点,CE与以BC为直径的半圆O交于点F,C
如图,正方形ABCD中,E是AB的中点,CE与以BC为直径的半圆O交于点F,C查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com