
【题目】若数列![]() 满足
满足![]() ,且存在常数
,且存在常数![]() ,使得对任意的
,使得对任意的![]() 都有
都有![]() ,则称数列
,则称数列![]() 为“k控数列”.
为“k控数列”.
(1)若公差为d的等差数列![]() 是“2控数列”,求d的取值范围;
是“2控数列”,求d的取值范围;
(2)已知公比为![]() 的等比数列
的等比数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 与
与![]() 都是“k控数列”,求q的取值范围(用k表示).
都是“k控数列”,求q的取值范围(用k表示).
【答案】(1)![]() (2)
(2)![]() .
.
【解析】
(1)根据“![]() 控数列”的定义得出
控数列”的定义得出![]() ,则由等差数列的通项公式可得
,则由等差数列的通项公式可得![]() 对
对![]() 恒成立,求出公差
恒成立,求出公差![]() 的取值范围;
的取值范围;
(2)由等比数列![]() 为“
为“![]() 控数列”得
控数列”得![]() ,又
,又![]() 是“
是“![]() 控数列”得
控数列”得![]() ,分类讨论求出q的取值范围.
,分类讨论求出q的取值范围.
(1)因为公差为![]() 的等差数列
的等差数列![]() 是“2控数列”,所以
是“2控数列”,所以![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以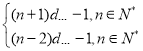
由![]() 得所以
得所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
由![]() 得:
得:
当![]() 时,
时,![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() 成立;
成立;
当![]() 时,
时,![]() ,又
,又![]() ,所以
,所以![]() ;
;
综上,![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() ;
;
(2)因为数列![]() 是公比为
是公比为![]() 的等比数列且为“
的等比数列且为“![]() 控数列”,所以
控数列”,所以![]() ,显然
,显然![]() ,故
,故![]() .
.
易知![]() ,要使
,要使![]() 是“
是“![]() 控数列”,
控数列”,
则![]() ,
,
(ⅰ)当![]() 时,
时,![]() ,
,
令![]() ,则
,则![]() 递减,
递减,
所以![]() ,
,
所以![]() ,即
,即![]() .
.
要使![]() 存在,则
存在,则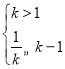 得
得![]() ;
;
(ⅱ)当![]() 时,
时,![]() ,
,
令![]() ,则
,则![]() 递减,
递减,![]() ,
,
所以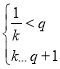 ,又
,又![]() ,所以
,所以![]() ,
,
要使![]() 存在,需
存在,需![]() ,得
,得![]()
综上,当![]() 时,公比
时,公比![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】平面直角坐标系中有16个格点(i,j),其中0≤i≤3,0≤j≤3.若在这16个点中任取n个点,这n个点中总存在4个点,这4个点是一个正方形的顶点,求n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线C1:x=﹣2以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,C2极坐标方程为:ρ2﹣2ρcosθ﹣4ρsinθ+4=0.
(1)求C1的极坐标方程和C2的普通方程;
(2)若直线C3的极坐标方程为![]() ,设C2与C3的交点为M,N,又C1:x=﹣2与x轴交点为H,求△HMN的面积.
,设C2与C3的交点为M,N,又C1:x=﹣2与x轴交点为H,求△HMN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆
,过椭圆![]() 的左、右焦点
的左、右焦点![]() 分别作倾斜角为
分别作倾斜角为![]() 的直线
的直线![]() ,且
,且![]() 之间的距离为1.
之间的距离为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 只有一个公共点,求点
只有一个公共点,求点![]() 到直线
到直线![]() 的距离之积.
的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2019年亚洲杯前,某商家为了鼓励中国球迷组团到阿联酋支持中国队,制作了3种精美海报,每份中国队球迷礼包中随机装入一份海报,每集齐3种不同的海报就可获得中国队在亚洲杯上所有比赛中的1张门票.现有6名中国队球迷组成的球迷团,每人各买一份中国队球迷礼包,则该球迷团至少获得1张门票的可能情况的种数为( )
A.360B.450C.540D.990
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把一块边长为![]() 的正六边形铁皮,沿图中的虚线(虛线与正六边形的对应边垂直)剪去六个全等的四边形(阴影部分),折起六个矩形焊接制成一个正六棱柱形的无盖容器(焊接损耗忽略),设容器的底面边长为
的正六边形铁皮,沿图中的虚线(虛线与正六边形的对应边垂直)剪去六个全等的四边形(阴影部分),折起六个矩形焊接制成一个正六棱柱形的无盖容器(焊接损耗忽略),设容器的底面边长为![]() .
.

(1)若![]() ,且该容器的表面积为
,且该容器的表面积为![]() 时,在该容器内注入水,水深为
时,在该容器内注入水,水深为![]() ,若将一根长度为
,若将一根长度为![]() 的玻璃棒(粗细忽略)放入容器内,一端置于
的玻璃棒(粗细忽略)放入容器内,一端置于![]() 处,另一端置于侧棱
处,另一端置于侧棱![]() 上,忽略铁皮厚度,求玻璃棒浸人水中部分的长度;
上,忽略铁皮厚度,求玻璃棒浸人水中部分的长度;
(2)求该容器的底面边长![]() 的范围,使得该容器的体积始终不大于
的范围,使得该容器的体积始终不大于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() ,
,![]() 分别是曲线
分别是曲线![]() ,
,![]() 上两动点且
上两动点且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,抛物线
,抛物线![]() 上存在一点M,使得直线AM的斜率的最大值为1,圆Q的方程为
上存在一点M,使得直线AM的斜率的最大值为1,圆Q的方程为![]() .
.
(1)求点M的坐标和C的方程;
(2)若直线l交C于D,E两点且直线MD,ME都与圆Q相切,证明直线l与圆Q相离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为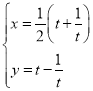 (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系.
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)写出曲线C的普通方程和极坐标方程;
(Ⅱ)M,N为曲线C.上两点,若OM⊥ON,求|MN|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com