
【题目】已知圆![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴非负半轴为极轴建立极坐标系,则曲线
轴非负半轴为极轴建立极坐标系,则曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程与
的普通方程与![]() 的直角坐标方程;
的直角坐标方程;
(2)点![]() 是曲线
是曲线![]() 上一点,由
上一点,由![]() 向圆
向圆![]() 引切线,切点分别为
引切线,切点分别为![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
科目:高中数学 来源: 题型:
【题目】某文体局为了解“跑团”每月跑步的平均里程,收集并整理了2018年1月至2018年11月期间“跑团”每月跑步的平均里程(单位:公里)的数据,绘制了下面的折线图.根据折线图,下列结论正确的是( )

A. 月跑步平均里程的中位数为6月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在8、9月
D. 1月至5月的月跑步平均里程相对于6月至11月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
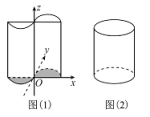
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图(1),函数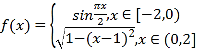 的图象与x轴围成一个封闭区域A(阴影部分),将区域A(阴影部分)沿z轴的正方向上移6个单位,得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示,其底面积与区域A(阴影部分)的面积相等,则此柱体的体积为______.
的图象与x轴围成一个封闭区域A(阴影部分),将区域A(阴影部分)沿z轴的正方向上移6个单位,得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示,其底面积与区域A(阴影部分)的面积相等,则此柱体的体积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(1﹣sinx)ex.
(1)求f(x)在区间(0,π)的极值;
(2)证明:函数g(x)=f(x)﹣sinx﹣1在区间(﹣π,π)有且只有3个零点,且之和为0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率;先由计算器给出0到9之间取整数值的随机数,指定0、1、2表示没有击中目标,3、4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20随机数:![]()
![]()
根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )
A.0.55B.0.6C.0.65D.0.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 是椭圆上一动点(与左、右顶点不重合)已知
是椭圆上一动点(与左、右顶点不重合)已知![]() 的内切圆半径的最大值为
的内切圆半径的最大值为![]() ,椭圆的离心率为
,椭圆的离心率为![]() .
.
(1)求椭圆C的方程;
(2)过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,过
两点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 与另一点
与另一点![]() (
(![]() 不与
不与![]() 重合).设
重合).设![]() 的外心为
的外心为![]() ,求证
,求证![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com