
数列{an}满足a1=1,an+1=(n2+n-λ)an(n=1,2,…),λ是常数.
(1)当a2=-1时,求λ及a3的值.
(2)数列{an}是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由.
(1) λ=3 a3=-3. (2) 不可能,理由见解析
【解析】(1)由于an+1=(n2+n-λ)an(n=1,2,…),
且a1=1,所以当a2=-1时,得-1=2-λ,
故λ=3.从而a3=(22+2-3)×(-1)=-3.
(2)数列{an}不可能为等差数列,理由如下:
由a1=1,an+1=(n2+n-λ)an,得
a2=2-λ,a3=(6-λ)(2-λ),
a4=(12-λ)(6-λ)(2-λ).
若存在λ,使{an}为等差数列,则a3-a2=a2-a1,
即(5-λ)(2-λ)=1-λ,解得λ=3.
于是a2-a1=1-λ=-2,
a4-a3=(11-λ)(6-λ)(2-λ)=-24.
这与{an}为等差数列矛盾.
所以,对任意λ,{an}都不可能是等差数列.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十五第六章第一节练习卷(解析版) 题型:选择题
若A=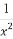 +3与B=
+3与B=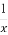 +2,则A,B的大小关系是( )
+2,则A,B的大小关系是( )
(A)A>B (B)A<B
(C)A≥B (D)不确定
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:解答题
等差数列{an}中,2a1+3a2=11,2a3=a2+a6-4,其前n项和为Sn.
(1)求数列{an}的通项公式.
(2)设数列{bn}满足bn=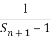 ,其前n项和为Tn,求证:Tn<
,其前n项和为Tn,求证:Tn< (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:填空题
已知x,y满足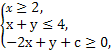 且目标函数z=3x+y的最小值是5,则z的最大值是 .
且目标函数z=3x+y的最小值是5,则z的最大值是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:选择题
已知变量x,y满足约束条件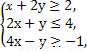 则目标函数z=3x-y的取值范围是( )
则目标函数z=3x-y的取值范围是( )
(A)[- ,6] (B)[-
,6] (B)[- ,-1]
,-1]
(C)[-1,6] (D)[-6, ]
]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十一第五章第二节练习卷(解析版) 题型:选择题
已知两个等差数列{an}和{bn}的前n项和分别为An和Bn,且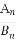 =
= ,则使得
,则使得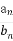 为整数的正整数n的个数是( )
为整数的正整数n的个数是( )
(A)2(B)3(C)4(D)5
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十一第五章第二节练习卷(解析版) 题型:选择题
已知等差数列{an}中,|a3|=|a9|,公差d<0,Sn是数列{an}的前n项和,则( )
(A)S5>S6(B)S5<S6
(C)S6=0(D)S5=S6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十第十章第七节练习卷(解析版) 题型:选择题
一学生通过一种英语听力测试的概率是 ,他连续测试两次,那么其中恰有一次通过的概率是( )
,他连续测试两次,那么其中恰有一次通过的概率是( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:解答题
为缓解某路段交通压力,计划将该路段实施“交通限行”.在该路段随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:
年龄 (岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频 数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成 人数 | 4 | 8 | 9 | 6 | 4 | 3 |
(1)作出被调查人员年龄的频率分布直方图.
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“交通限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com