
| A. | $({0,\frac{1}{e}})$ | B. | $({\frac{1}{e},1})$ | C. | (1,e) | D. | (e,+∞) |
分析 函数f(x)=lnx+ex在(0,+∞)上单调递增,因此函数f(x)最多只有一个零点.再利用函数零点存在判定定理即可判断出.
解答 解:函数f(x)=lnx+ex在(0,+∞)上单调递增,因此函数f(x)最多只有一个零点.
当x→0+时,f(x)→-∞;又$f(\frac{1}{e})$=$ln\frac{1}{e}$+${e}^{\frac{1}{e}}$=${e}^{\frac{1}{e}}$-1>0,
∴函数f(x)=lnx+ex(e为自然对数的底数)的零点所在的区间是$(0,\frac{1}{e})$.
故选:A.
点评 本题考查了函数零点存在判定定理、函数的单调性,考查了推理能力与计算能力,属于中档题.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2 | B. | f(x)=2|x| | C. | f(x)=log2$\frac{1}{|x|}$ | D. | f(x)=sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{9}$ | B. | $\frac{8}{27}$ | C. | $\frac{4}{27}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
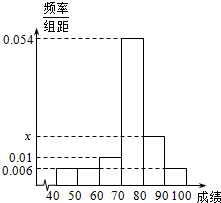 某班50位学生2015届中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
某班50位学生2015届中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com