练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

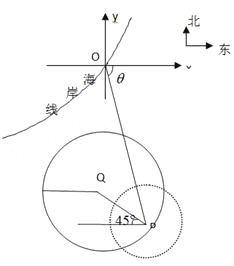
    【题目】在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O（如图）的东偏南方向300km的海面P处，并以20km/h的速度向西偏北方向移动，台风侵袭的范围为圆形区域，当前半径为60km，并以10km/h的速度不断增大，问几小时后该城市开始受到台风的侵袭？

    【答案】12小时后该城市开始受到台风的侵袭

    【解析】

    设在t时刻台风中心位于点Q，此时|OP|=300，|PQ|=20t，

    台风侵袭范围的圆形区域半径为10t+60，

    由，可知，

    cos∠OPQ=cos(θ-45o)= cosθcos45o+sinθsin45o=

    在 △OPQ中，由余弦定理，得

    =

    =

    若城市O受到台风的侵袭，则有|OQ|≤r(t)，即

    ，

    整理，得，解得12≤t≤24,

    答：12小时后该城市开始受到台风的侵袭.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设的内角A，B，C的对边长a，b，c成等比数列，，延长BC至D，若，则面积的最大值为（ ）

    A.2B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】当我们所处的北半球为冬季的时候，新西兰的惠灵顿市恰好是盛夏，因此北半球的人们冬天愿意去那里旅游，下面是一份惠灵顿机场提供的月平均气温统计表.

    （月份）

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    17.3

    17.9

    17.3

    15.8

    13.7

    11.6

    10.06

    9.5

    10.06

    11.6

    13.7

    15.8

    （1）根据这个统计表提供的数据，为惠灵顿市的月平均气温作出一个函数模型；

    （2）当自然气温不低于13.7℃时，惠灵顿市最适宜旅游，试根据你所确定的函数模型，确定惠灵顿市的最佳旅游时间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）讨论函数的单调区间；

    （2）若恒成立，求实数的取值范围；

    （3）证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AB是圆的直径，PA垂直圆所在的平面，C是圆上的点．

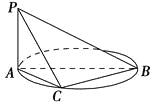
    (1)求证：平面PAC⊥平面PBC；

    (2)若AB＝2，AC＝1，PA＝1，求二面角C－PB－A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题正确的是（ ）

    A.经过任意三点有且只有一个平面.

    B.过点有且仅有一条直线与异面直线垂直.

    C.一条直线与一个平面平行，它就和这个平面内的任意一条直线平行.

    D.面与平面相交，则公共点个数为有限个.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】十九大提出，加快水污染防治，建设美丽中国.根据环保部门对某河流的每年污水排放量（单位：吨）的历史统计数据，得到如下频率分布表：

    将污水排放量落入各组的频率作为概率，并假设每年该河流的污水排放量相互独立.

    （1）求在未来3年里，至多1年污水排放量的概率；（2）该河流的污水排放对沿河的经济影响如下：当时，没有影响；当时，经济损失为10万元；当时，经济损失为60万元.为减少损失，现有三种应对方案：

    方案一：防治350吨的污水排放，每年需要防治费3.8万元；

    方案二：防治310吨的污水排放，每年需要防治费2万元；

    方案三：不采取措施.

    试比较上述三种文案，哪种方案好，并请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若、是两个相交平面，则在下列命题中，真命题的序号为（ ）

    ①若直线，则在平面内一定不存在与直线平行的直线．

    ②若直线，则在平面内一定存在无数条直线与直线垂直．

    ③若直线，则在平面内不一定存在与直线垂直的直线．

    ④若直线，则在平面内一定存在与直线垂直的直线．

    A. ①③ B. ②③ C. ②④ D. ①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某电信公司为了加强新用5G技术的推广使用，为该公司的用户制定了一套5G月消费返流量费的套餐服务方案；当月消费金额不超过100元时，按消费金额的进行返还；当月消费金额超过100元时，除消费金额中的100元仍按进行返还外，若另超出100元的部分消费金额为A元，则超过部分按进行返还，记用户当月返还所得流量费y(单位:元)，消费金额x(单位:元)

    （1）写出该公司用户月返还所得流量费的函数模型；

    （2）如果用户小李当月获返还的流量费是12元，那么他这个月的消费金额是多少元?

    查看答案和解析>>

    同步练习册答案