
 ,且
,且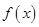 在
在 处取得极值.
处取得极值. 的值;
的值;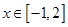 时,
时,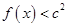 恒成立,求
恒成立,求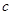 的取值范围;
的取值范围;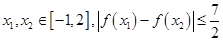 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由. 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源:不详 题型:解答题
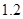 万件、
万件、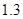 万件,为了估测当年每个月的产量,以这三个月的产品数量为依据,用一个函数模型模拟该产品的月产量
万件,为了估测当年每个月的产量,以这三个月的产品数量为依据,用一个函数模型模拟该产品的月产量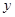 与月份
与月份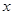 的关系,模拟函数可选用函数
的关系,模拟函数可选用函数 (其中
(其中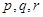 为常数)或二次函数。又已知当年4月份该产品的产量为
为常数)或二次函数。又已知当年4月份该产品的产量为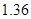 万件,请问用以上哪个函数作为模拟函数较好,并说明理由。
万件,请问用以上哪个函数作为模拟函数较好,并说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
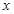 个月的利润
个月的利润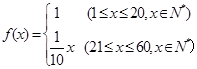 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第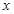 个月的当月利润率
个月的当月利润率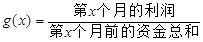 ,例如:
,例如: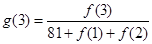 .
.  求
求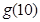 ; (Ⅱ)求第
; (Ⅱ)求第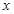 个月的当月利润率
个月的当月利润率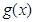 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com