
【题目】下列命题中所有正确的序号是____.
(1)![]() ,对应
,对应![]() :
:![]() 是映射;
是映射;
(2)函数![]() 和
和![]() 都是既奇又偶函数;
都是既奇又偶函数;
(3)已知对任意的非零实数![]() 都有
都有![]() ,则
,则![]() ;
;
(4)函数![]() 的定义域是
的定义域是![]() ,则函数
,则函数![]() 的定义域为
的定义域为![]() ;
;
(5)函数![]() 在
在![]() 和
和![]() 上都是增函数,则函数
上都是增函数,则函数![]() 在
在![]() 上一定是增函数.
上一定是增函数.
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 是椭圆
是椭圆![]() 上的两点,且
上的两点,且![]() ,其中
,其中![]() 为椭圆的右焦点.
为椭圆的右焦点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() ,使得
,使得![]() 为定值?若存在,求出定值和定点坐标;若不存在,说明理由.
为定值?若存在,求出定值和定点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1的方程为![]() ,双曲线C2的左、右焦点分别是C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点,O为坐标原点.
,双曲线C2的左、右焦点分别是C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点,O为坐标原点.
(1)求双曲线C2的方程;
(2)若直线l:y=kx+![]() 与双曲线C2恒有两个不同的交点A和B,且
与双曲线C2恒有两个不同的交点A和B,且![]() ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实力相等的甲、乙两队参加乒乓球团体比 赛,规定5局3胜制(即5局内谁先赢3局就算胜出并停止比赛).
⑴试求甲打完5局才能取胜的概率.
⑵按比赛规则甲获胜的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设两实数![]() 不相等且均不为
不相等且均不为![]() .若函数
.若函数![]() 在
在![]() 时,函数值
时,函数值![]() 的取值区间恰为
的取值区间恰为![]() ,就称区间
,就称区间![]() 为
为![]() 的一个“倒域区间”.已知函数
的一个“倒域区间”.已知函数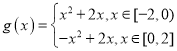 .
.
(1)求函数![]() 在
在![]() 内的“倒域区间”;
内的“倒域区间”;
(2)若函数![]() 在定义域
在定义域![]() 内所有“倒域区间”的图象作为函数
内所有“倒域区间”的图象作为函数![]() 的图象,是否存在实数
的图象,是否存在实数![]() ,使得
,使得![]() 与
与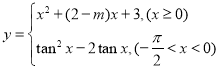 恰好有2个公共点?若存在,求出
恰好有2个公共点?若存在,求出![]() 的取值范围:若不存在,请说明理由.
的取值范围:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求满足
时,求满足![]() 的
的![]() 的取值;
的取值;
(2)若函数![]() 是定义在
是定义在![]() 上的奇函数
上的奇函数
①存在![]() ,不等式
,不等式![]() 有解,求
有解,求![]() 的取值范围;
的取值范围;
②若函数![]() 满足
满足![]() ,若对任意
,若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四名同学各掷骰子5次,分别记录每次骰子出现的点数,根据四名同学的统计结果,可以判断出一定没有出现点数6的是( )
A.平均数为3.中位数为2B.中位数为3.众数为2
C.平均数为2.方差为2.4D.中位数为3.方差为2.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com