
| 3 |
| 3 |
| 3 |
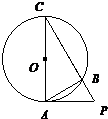 解:(1)依题意,我们知道△PBA∽△PAC,
解:(1)依题意,我们知道△PBA∽△PAC,| PA |
| 2R |
| PB |
| AB |
| PA•AB |
| 2PB |
2
| ||
| 2×1 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 4 |
| ||
| 2 |
| ||
| 2 |
(
|


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:
 (考生注意:请在下面两题中任选一题作答,如果都做,则按所做第1题评分)
(考生注意:请在下面两题中任选一题作答,如果都做,则按所做第1题评分)
|
|
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2010年浙江省宁波市八校联考高二第二学期期末数学(理)试题 题型:解答题
(请考生在下面甲、乙两题中任选一题做答,如果多做,则按所做的甲题计分)
甲题 :
(1)若关于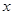 的不等式
的不等式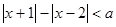 的解集不是空集,求实数
的解集不是空集,求实数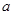 的取值范围;
的取值范围;
(2)已知实数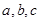 ,满足
,满足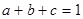 ,求
,求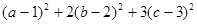 最小值.
最小值.
乙题:
已知曲线C的极坐标方程是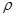 =4cos
=4cos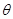 。以极点为平面直角坐标系的原点,极轴为
。以极点为平面直角坐标系的原点,极轴为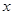 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线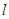 的参数方程是
的参数方程是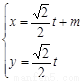 (
(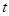 是参数)。
是参数)。
(1)将曲线C的极坐标方程化成直角坐标方程并把直线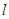 的参数方程转化为普通方程;
的参数方程转化为普通方程;
(2) 若过定点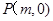 的直线
的直线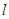 与曲线C相交于A、B两点,且
与曲线C相交于A、B两点,且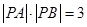 ,试求实数
,试求实数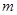 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2012年湖北省黄冈市英山一中高考数学模拟试卷1(理科)(解析版) 题型:解答题
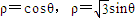 ,则此两圆的圆心距为 .
,则此两圆的圆心距为 .查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省黄冈市黄州一中高三(下)高考交流数学试卷(理科)(解析版) 题型:解答题
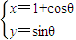 (θ为参数)上的点到曲线C2:
(θ为参数)上的点到曲线C2: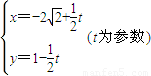 上的点的最短距离为 .
上的点的最短距离为 .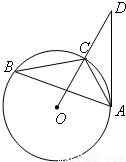
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com