
【题目】已知函数![]() .
.
(1)求![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 与
与![]() 在
在![]() 内恰有一个交点,求实数
内恰有一个交点,求实数![]() 的取值范围;
的取值范围;
(3)令![]() ,如果
,如果![]() 图象与
图象与![]() 轴交于
轴交于![]() ,
,![]() 中点为
中点为![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】
(1)利用导数的几何意义,求出斜率和切点,然后再根据点斜式即可求出结果;
(2)利用导数求出函数在![]() 的单调性,根据函数的单调性做出草图,即可求出实数
的单调性,根据函数的单调性做出草图,即可求出实数![]() 的取值范围;
的取值范围;
(3)由点![]() 在
在![]() 图象上,把点的坐标代入
图象上,把点的坐标代入![]() 的解析式得方程组,两式相减得关于
的解析式得方程组,两式相减得关于![]() 的方程,假设
的方程,假设![]() 成立,求导,得关于
成立,求导,得关于![]() 的方程,由中点坐标公式转化关于
的方程,由中点坐标公式转化关于![]() 的方程,两方程消去
的方程,两方程消去![]() ,得关于
,得关于![]() 的方程,整理此方程,分子分母同除以
的方程,整理此方程,分子分母同除以![]() ,整理方程,右边为
,整理方程,右边为![]() ,设
,设![]() ,左边得关于
,左边得关于![]() 的函数,求此函数的导数,得函数的单调性,得函数值恒小于
的函数,求此函数的导数,得函数的单调性,得函数值恒小于![]() ,所以方程不成立,所以假设不成立,所以
,所以方程不成立,所以假设不成立,所以![]() .
.
(1)![]() ,
,
则![]() ,且切点坐标为
,且切点坐标为![]() ;
;
所以所求切线方程为:![]()
(2)![]() ,所以
,所以![]() 在
在![]() 为增函数,在
为增函数,在![]() 为减函数,
为减函数,
![]() ,
, ![]() ;
;
所以![]()
(3)![]() ,
,![]() , 假设
, 假设![]() ,则有
,则有
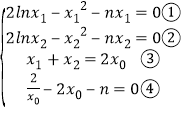
①-②得:![]() ∴
∴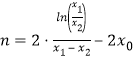 ,
,
由④得![]() , ∴
, ∴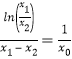 ;即
;即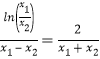 ;
;
即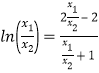 ⑤; 令
⑤; 令![]() ,
,![]() ,
,
则![]() 在0<t<1上增函数.
在0<t<1上增函数.![]() .∴⑤式不成立,故与假设矛盾.∴
.∴⑤式不成立,故与假设矛盾.∴![]() .
.


科目:高中数学 来源: 题型:
【题目】公元2020年春,我国湖北武汉出现了新型冠状病毒,人感染后会出现发热、咳嗽、气促和呼吸困难等,严重的可导致肺炎甚至危及生命.为了尽快遏制住病毒的传播,我国科研人员,在研究新型冠状病毒某种疫苗的过程中,利用小白鼠进行科学试验.为了研究小白鼠连续接种疫苗后出现![]() 症状的情况,决定对小白鼠进行做接种试验.该试验的设计为:①对参加试验的每只小白鼠每天接种一次;②连续接种三天为一个接种周期;③试验共进行3个周期.已知每只小白鼠接种后当天出现症状的概率均为
症状的情况,决定对小白鼠进行做接种试验.该试验的设计为:①对参加试验的每只小白鼠每天接种一次;②连续接种三天为一个接种周期;③试验共进行3个周期.已知每只小白鼠接种后当天出现症状的概率均为![]() ,假设每次接种后当天是否出现
,假设每次接种后当天是否出现![]() 症状与上次接种无关.
症状与上次接种无关.
(1)若某只小白鼠出现![]() 症状即对其终止试验,求一只小白鼠至多能参加一个接种周期试验的概率;
症状即对其终止试验,求一只小白鼠至多能参加一个接种周期试验的概率;
(2)若某只小白鼠在一个接种周期内出现2次或3次![]() 症状,则在这个接种周期结束后,对其终止试验.设一只小白鼠参加的接种周期为
症状,则在这个接种周期结束后,对其终止试验.设一只小白鼠参加的接种周期为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,椭圆的一个顶点为
轴上,椭圆的一个顶点为![]() ,右焦点
,右焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,且
,且![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,
两点,![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,求四边形
两点,求四边形![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,
中,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,BC//AD,已知Q是四边形ABCD内部一点,且二面角
,BC//AD,已知Q是四边形ABCD内部一点,且二面角![]() 的平面角大小为
的平面角大小为![]() ,若动点Q的轨迹将ABCD分成面积为
,若动点Q的轨迹将ABCD分成面积为![]() 的两部分,则
的两部分,则![]() =_______.
=_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知双曲线![]() 设过点
设过点![]() 的直线l的方向向量
的直线l的方向向量![]()
(1) 当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;
(2) 证明:当![]() >
>![]() 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
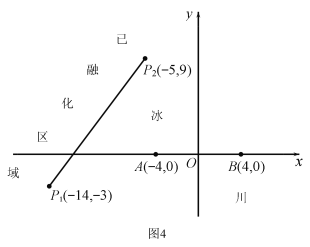
【题目】为了考察冰川的融化状况,一支科考队在某冰川山上相距8km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(图4).考察范围到A、B两点的距离之和不超过10km的区域.
(I)求考察区域边界曲线的方程:
(II)如图4所示,设线段![]() 是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍.问:经过多长时间,点A恰好在冰川边界线上?
是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍.问:经过多长时间,点A恰好在冰川边界线上?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为
的右顶点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的离心率为
.已知椭圆的离心率为![]() ,
,![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设直线![]() :
:![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,且点
两点,且点![]() 在第二象限.
在第二象限.![]() 与
与![]() 延长线交于点
延长线交于点![]() ,若
,若![]() 的面积是
的面积是![]() 面积的3倍,求
面积的3倍,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com