
【题目】平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的焦点为F,过F的直线
的焦点为F,过F的直线![]() 交
交![]() 于B,C两点.
于B,C两点.
(1)若![]() 垂直于轴,且线段BC的长为1,求
垂直于轴,且线段BC的长为1,求![]() 的方程;
的方程;
(2)若![]() 的斜率为
的斜率为![]() ,求
,求![]() ;
;
(3)设抛物线上异于![]() 的点A满足
的点A满足![]() ,若
,若![]() 的重心在
的重心在![]() 轴上,求
轴上,求![]() 的重心的坐标.
的重心的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)直线![]() 方程为
方程为![]() ,与抛物线方程联立,可得交点
,与抛物线方程联立,可得交点![]() 坐标,从而得
坐标,从而得![]() ,由此可求得
,由此可求得![]() ,得抛物线方程;
,得抛物线方程;
(2)设![]() ,不妨设
,不妨设![]() 在第一象限,
在第一象限,![]() 在第四象限,即
在第四象限,即![]()
![]() ,直线
,直线![]() 方程为
方程为![]() ,
,![]() .求出
.求出![]() ,
,![]() ,再由直线方程与抛物线方程联立,消去
,再由直线方程与抛物线方程联立,消去![]() 后可得
后可得![]() ,代入
,代入![]() 中,可得结论;
中,可得结论;
(3)分类,![]() 与
与![]() 轴垂直,重心为
轴垂直,重心为![]() ;
;![]() 与
与![]() 轴不垂直,与(2)一样,设方程为
轴不垂直,与(2)一样,设方程为![]()
![]() ,
,![]() ,仿(2)得
,仿(2)得![]() ,重心在
,重心在![]() 轴.则有
轴.则有
![]() ,从而可得
,从而可得![]() ,于是也有
,于是也有![]() ,设
,设![]() 中点为
中点为![]() ,由中点坐标公式求得
,由中点坐标公式求得![]() ,利用
,利用![]() 可求得
可求得![]() ,最终可得出直线
,最终可得出直线![]() 方程,它与
方程,它与![]() 交点为所求重心.
交点为所求重心.
(1)由 ,∴
,∴![]() ,
,
∴抛物线![]() 的方程为:
的方程为:![]() ;
;
(2)设![]() ,不妨设
,不妨设![]() 在第一象限,
在第一象限,![]() 在第四象限,即
在第四象限,即![]()
![]() ,直线
,直线![]() 方程为
方程为![]() ,
,![]() .
.
∵![]() ,
,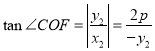 ,
,
∴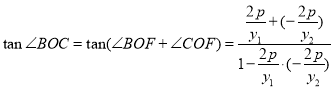
![]() ,
,
由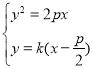 得
得![]() ,∴
,∴![]() ,
,![]() .
.
∴![]()
![]()
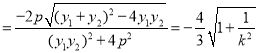 ;
;
(3)若![]() 垂直于
垂直于![]() 轴,则由
轴,则由![]() 得
得![]() ,此时重心坐标为
,此时重心坐标为![]() .
.
若直线![]() 与
与![]() 轴不垂直,设方程为
轴不垂直,设方程为![]()
![]() ,
,![]() ,
,
则![]() ,由(2)
,由(2)![]() ,∴
,∴![]() ,
,![]() ,
,
设线段![]() 中点为
中点为![]() ,
,
则![]() ,
,![]() ,
,
∴直线![]() 斜率为
斜率为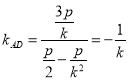 (与
(与![]() 垂直),∴
垂直),∴![]() ,
,![]() ,
,
此时![]() ,从而直线
,从而直线![]() 方程为
方程为![]() ,它与
,它与![]() 轴交点为
轴交点为![]() ,此即为所求重心坐标.
,此即为所求重心坐标.
综上,![]() 的重心为
的重心为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】2016年1月6日,中国物流与采购联合会正式发布了中国仓储指数,中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的一套指数体系,如图所示的折线图是2019年甲企业和乙企业的仓储指数走势情况.根据该折线图,下列结论中不正确的是( )
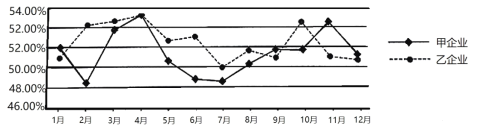
A.2019年1月至4月甲企业的仓储指数比乙企业的仓储指数波动大
B.甲企业2019年的年平均仓储指数明显低于乙企业2019年的年平均仓储指数
C.两企业2019年的最大仓储指数都出现在4月份
D.2019年7月至9月乙企业的仓储指数的增幅高于甲企业
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应国家号召,某校组织部分学生参与了“垃圾分类,从我做起”的知识问卷作答,并将学生的作答结果分为“合格”与“不合格”两类与“问卷的结果”有关?
不合格 | 合格 | |
男生 | 14 | 16 |
女生 | 10 | 20 |
(1)是否有90%以上的把握认为“性别”与“问卷的结果”有关?
(2)在成绩合格的学生中,利用性别进行分层抽样,共选取9人进行座谈,再从这9人中随机抽取5人发送奖品,记拿到奖品的男生人数为X,求X的分布列及数学期望![]() .
.
附: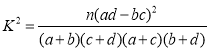
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.703 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() ,已知函数
,已知函数![]() 、
、![]() 定义域都是
定义域都是![]() ,给出下列命题:
,给出下列命题:
(1)若![]() 、
、![]() 都是奇函数,则函数
都是奇函数,则函数![]() 为奇函数;
为奇函数;
(2)若![]() 、
、![]() 都是减函数,则函数
都是减函数,则函数![]() 为减函数;
为减函数;
(3)若![]() ,
,![]() ,则
,则![]() ;
;
(4)若![]() 、
、![]() 都是周期函数,则函数
都是周期函数,则函数![]() 是周期函数.
是周期函数.
其中正确命题的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() (
(![]() 为常数).
为常数).
(i)给出下列结论:
①曲线![]() 为中心对称图形;
为中心对称图形;
②曲线![]() 为轴对称图形;
为轴对称图形;
③当![]() 时,若点
时,若点![]() 在曲线
在曲线![]() 上,则
上,则![]() 或
或![]() .
.
其中,所有正确结论的序号是_________.
(ii)当![]() 时,若曲线
时,若曲线![]() 所围成的区域的面积小于
所围成的区域的面积小于![]() ,则
,则![]() 的值可以是_________.(写出一个即可)
的值可以是_________.(写出一个即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{2n﹣1}的前n项1,3,7,…,2n﹣1组成集合![]() (n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
(n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com