练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知α，β∈(0，)且满足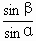＝cos(α＋β)．

    (1)求证：tanβ＝．

    (2)求tanβ的最大值，并求当tanβ取得最大值时，tan(α＋β)的值．

    答案：
    解析：

    		 　　解：(1)因为 ＝cos(α＋β)，所以sinβ＝sinαcosαcosβ－sin2αsinβ

    　　解：(1)因为＝cos(α＋β)，所以sinβ＝sinαcosαcosβ－sin2αsinβ．所以＝sinαcosα－sin2α．即tanβ＝sinαcosα－sin2αtanβ．

    　　所以tanβ(1＋sin2α)＝sinαcosα．所以tanβ＝．

    　　(2)tanβ＝＝＝．因为α∈(0，)，所以tanα＞0．所以tanβ＝＝≤．当且仅当2tanα＝，即tanα＝时，tanβ取最大值，最大值为＝．此时tan(α＋β)＝＝．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：中学教材标准学案　数学　高二上册 题型：044

    解答题

    已知两点A(2，0)，B(－2，0)，动点P满足|PA|＝2|PB|，求点P的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    解答题

    已知函数f(x)的定义域是R，对任意x、y∈R，都有f(x＋y)＝f(x)＋f(y)，且x>0时，f(x)<0，f(1)＝－2，求f(x)在[－3，3]上的最大值和最小值．

     

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    已知M＝(1＋cos2x，1)，N＝(1，sin2x＋a)，(x∈R，a∈R，a是常数)，且y＝(O为坐标原点)

    (1)求y关于x的函数关系式y＝f(x)；

    (2)若x∈[0，]时，f(x)的最大值为4，求a的值，并说明此时f(x)的图像可由y＝2sin(x＋)的图像经过怎样的变换而得到．

    查看答案和解析>>

    科目：高中数学 来源：2007龙门中学、新丰一中、连平中学三校联考试题、高三数学(文) 题型：044

    解答题

    已知函数恒过点．

    (1)

    求的值；

    (2)

    求函数的最小正周期及单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源：安徽省示范高中铜陵三中2006－2007学年度高三数学理科第一次诊断性考试卷 新课标 人教版 人教版新课标 题型：044

    解答题

    已知，设命题：和是方程的两个实根，不等式对任意实数恒成立；Q：函数在区间(－¥ ，＋¥ )上有极值．求使P正确且Q正确的m的取值范围

    查看答案和解析>>

    同步练习册答案