
已知f(1,1)=1,f(m,n)∈N*(m,n∈N*),且对任意的m,n∈N*都有:
(1)f(m,n+1)=f(m,n)+2.
(2)f(m+1,1)=2f(m,1).
给出以下三个结论:①f(1,5)=9;②f(5,1)=16;
③f(5,6)=26.其中正确结论的序号有 .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷(解析版) 题型:选择题
一个锥体的正视图和侧视图如图所示,下面选项中,不可能是该锥体的俯视图的是( )
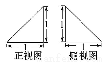
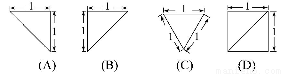
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:选择题
正方体ABCD-A1B1C1D1的棱长为a,点M在AC1上且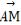 =
=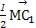 ,N为B1B的中点,则|
,N为B1B的中点,则| |为( )
|为( )
(A)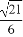 a (B)
a (B) a (C)
a (C) a (D)
a (D) a
a
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:填空题
用数学归纳法证明1+ +
+ +…+
+…+ <n(n∈N*,n>1)时,第一步应验证的不等式是 .
<n(n∈N*,n>1)时,第一步应验证的不等式是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:选择题
已知n是正偶数,用数学归纳法证明时,若已假设n=k(k≥2且为偶数)时命题为真,则还需证明( )
(A)n=k+1时命题成立
(B)n=k+2时命题成立
(C)n=2k+2时命题成立
(D)n=2(k+2)时命题成立
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十 第六章第六节练习卷(解析版) 题型:选择题
若|loga |=loga
|=loga ,|logba|=-logba,则a,b满足的条件是( )
,|logba|=-logba,则a,b满足的条件是( )
(A)a>1,b>1 (B)0<a<1,b>1
(C)a>1,0<b<1 (D)0<a<1,0<b<1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十第二章第七节练习卷(解析版) 题型:填空题
若函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[-1,1)时,f(x)=|x|,则函数y=f(x)的图象与函数y=log4|x|的图象的交点的个数为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十五第二章第十二节练习卷(解析版) 题型:解答题
已知函数f(x)=x3-3x.
(1)求函数f(x)的单调区间.
(2)求函数f(x)在区间[-3,2]上的最值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com