

| A.0 | B. 1 | C. 2 | D. 3 |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
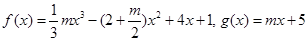 .
.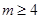 时,求
时,求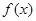 的单调递增区间;
的单调递增区间;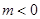 ,使得对任意的
,使得对任意的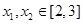 ,都有
,都有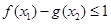 恒成立.若存在,求出
恒成立.若存在,求出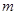 的取值范围; 若不存在,请说明理由.
的取值范围; 若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (单位:万元)随销售利润
(单位:万元)随销售利润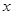 (单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不能超过利润的
(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不能超过利润的 %.现有三个奖励模型:
%.现有三个奖励模型: ,分析与推导哪个函数模型能符合该公司的要求?并给予证明.(注:
,分析与推导哪个函数模型能符合该公司的要求?并给予证明.(注: )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com