
【题目】已知椭圆C:![]() (
(![]() )的离心率为
)的离心率为![]() ,且椭圆C的中心O关于直线
,且椭圆C的中心O关于直线![]() 的对称点落在直线
的对称点落在直线![]() 上.
上.
(1)求椭圆C的方程;
(2)设P![]() ,M、N是椭圆C上关于x轴对称的任意两点,连接
,M、N是椭圆C上关于x轴对称的任意两点,连接![]() 交椭圆C于另一点E,求直线
交椭圆C于另一点E,求直线![]() 的斜率取值范围,并证明直线
的斜率取值范围,并证明直线![]() 与x轴相交于定点.
与x轴相交于定点.
科目:高中数学 来源: 题型:
【题目】在三棱锥S-ABC中,侧棱SA,SB,SC两两成等角,且长度分别为a,b,c,设二面角S-BC-A,S-AC–B,S-AB-C的大小为![]() ,若
,若![]() 则α,β,γ的大小关系是( )
则α,β,γ的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,![]() ,_________,DC=2,在下面给出的三个条件中任选一个,补充在上面的问题中,并加以解答.(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)①
,_________,DC=2,在下面给出的三个条件中任选一个,补充在上面的问题中,并加以解答.(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)①![]() ;②
;②![]() ;③
;③![]() .
.
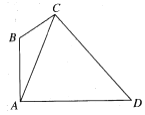
(1)求![]() 的大小;
的大小;
(2)求△ADC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,设点
,设点![]() 为圆
为圆![]() 与
与![]() 轴负半轴的交点,点
轴负半轴的交点,点![]() 为圆
为圆![]() 上一点,且满足
上一点,且满足![]() 的中点在
的中点在![]() 轴上.
轴上.
(1)当![]() 变化时,求点
变化时,求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,
,![]() 、
、![]() 为曲线
为曲线![]() 上两个不同的点,且在
上两个不同的点,且在![]() 、
、![]() 两点处的切线的交点在直线
两点处的切线的交点在直线![]() 上,证明:直线
上,证明:直线![]() 过定点,并求此定点坐标.
过定点,并求此定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校高三年级有1000人参加一次数学模拟考试,现把这次考试的分数转换为标准分,标准分的分数转换区间为![]() ,若使标准分X服从正态分布N
,若使标准分X服从正态分布N![]() ,则下列说法正确的有( ).
,则下列说法正确的有( ).
参考数据:①![]() ;②
;②![]() ;③
;③![]()
A.这次考试标准分超过180分的约有450人
B.这次考试标准分在![]() 内的人数约为997
内的人数约为997
C.甲、乙、丙三人恰有2人的标准分超过180分的概率为![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】整数集就像一片浩瀚无边的海洋,充满了无尽的奥秘.古希腊数学家毕达哥拉斯发现220和284具有如下性质:220的所有真因数之和恰好等于284,同时284的所有真因数之和也等于220,他把具有这种性质的两个整数叫做一对“亲和数”,“亲和数”的发现吸引了古今中外无数数学爱好者的研究热潮.已知220和284,1184和1210,2924和2620是3对“亲和数”,把这六个数随机分成两组,一组2个数,另一组4个数,则220和284在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com