
分析 先解已知不等式,再利用解得的区间长度与区间[0,2]的长度求比值即得.
解答 解:利用几何概型,其测度为线段的长度.
∵-1≤log${\;}_{\frac{1}{2}}$(x+$\frac{1}{2}$)≤1
∴$\frac{1}{2}$≤x+$\frac{1}{2}$≤2
解得0≤x≤$\frac{3}{2}$,
∵0≤x≤2
∴0≤x≤$\frac{3}{2}$
∴所求的概率为:P=$\frac{\frac{3}{2}}{2}$=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题主要考查了几何概型,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
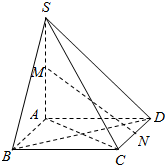 如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA⊥平面ABCD,M,N分别为SA,CD的中点.
如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA⊥平面ABCD,M,N分别为SA,CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
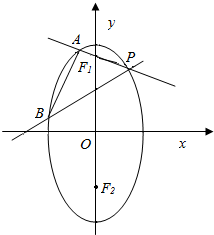 已知椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)的两个焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,直线$y=\sqrt{2}$过椭圆的焦点,点P是椭圆上位于第一象限的点,并满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=1$,过P作倾斜角互补的两条直线PA,PB分别交椭圆于A,B两点.
已知椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)的两个焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,直线$y=\sqrt{2}$过椭圆的焦点,点P是椭圆上位于第一象限的点,并满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=1$,过P作倾斜角互补的两条直线PA,PB分别交椭圆于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,3] | B. | (-6,1] | C. | (-∞,-1)∪(6,+∞) | D. | (-∞,-6)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1<a | B. | 1<a≤3 | C. | 1<a≤$\frac{5}{2}$ | D. | a≥3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com