
分析 (1)由正弦函数的最值,分别求得a和b的值,求得函数y=-2sin3x,利用正弦函数的性质,即可求得函数的周期,最值及相应的x的取值集合;
(2)由(1)可知$f(x)=2sin(\frac{π}{6}-2x)=-2sin(2x-\frac{π}{6})$,利用正弦函数的性质就看求得函数f(x)单调区间.
解答 解:(1)由题意知$\left\{{\begin{array}{l}{a+b=\frac{3}{2}}\\{a-b=-\frac{1}{2}}\end{array}}\right.$,解得$\left\{{\begin{array}{l}{a=\frac{1}{2}}\\{b=1}\end{array}}\right.$,∴y=-2sin3x,
∴$周期T=\frac{2π}{3}$,$当3x=2kπ+\frac{π}{2},即x∈\left\{{\left.x\right|x=\frac{2kπ}{3}+\frac{π}{6},k∈Z}\right\}时,{y_{min}}=-2$,
$当3x=2kπ-\frac{π}{2},即x∈\left\{{\left.x\right|x=\frac{2kπ}{3}-\frac{π}{6},k∈Z}\right\}时,{y_{max}}=2$
(2)由(1)知$f(x)=2sin(\frac{π}{6}-2x)=-2sin(2x-\frac{π}{6})$,
$令2kπ-\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{π}{2}则kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3}$,
$令2kπ+\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{3π}{2}则kπ+\frac{π}{3}≤x≤kπ+\frac{5π}{6}$,
∴函数f(x)的单调递减区间为[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z;
函数的单调递增区间[kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$],k∈Z.
点评 本题考查正弦函数的性质,考查正弦函数的单调性及最值,考查计算能力,属于中档题.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了了解高中生的身体健康情况,体育局随机抽取了某校20名学生的体育测试成绩,得到如图所示的茎叶图:
为了了解高中生的身体健康情况,体育局随机抽取了某校20名学生的体育测试成绩,得到如图所示的茎叶图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小值9 | B. | 最大值9 | C. | 最小值$5+2\sqrt{2}$ | D. | 最大值$5+2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
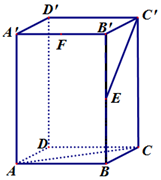 如图长方体ABCD-A'B'C'D'中,AB=BC=1,AA'=2,E、F分别是BB′、A'B'的中点.
如图长方体ABCD-A'B'C'D'中,AB=BC=1,AA'=2,E、F分别是BB′、A'B'的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{6}{5}$ | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com