
【题目】在一条公路上,每隔100km有个仓库(如图),共有5个仓库.一号仓库存有10t货物,二号仓库存20t,五号仓库存40t,其余两个仓库是空的.现在想把所有的货物放在一个仓库里,如果每吨货物运输1km需要0.5元运输费,那么要多少才行? ![]()
【答案】解:以一号仓库为原点建立坐标轴,
则五个点坐标分别为A1:0,A2:100,A3:200,A4:300,A5:400,
设货物集中于点B:x , 则所花的运费y=5|x|+10|x﹣100|+20|x﹣200|,
当0≤x≤100时,y=﹣25x+9000,此时,当x=100时,ymin=6500;
当100<x<200时,y=﹣5x+7000,此时,5000<y<6500;
当x≥200时,y=35x﹣9000,此时,当x=200时,ymin=5000.
综上可得,当x=200时,ymin=5000,
即将货物都运到五号仓库时,花费最少,为5000元.
【解析】要求把所有的货物放在一个仓库里运费最少,其实就是要求运输的总路程最少.先把实际问题转化为数学问题,以一号仓库为原点建立坐标轴,表示五个仓库的坐标,然后假设货物集中于某一点坐标设为x , 利用绝对值的意义表示出总运费y.然后根据x的取值范围化简绝对值得到y与x的分段函数,分别求出各段的最小值,最后比较去最小得解.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax﹣lnx,a∈R
(1)若函数f(x)在[1,2]上是减函数,求实数a的取值范围
(2)令g(x)=f(x)﹣x2 , 是否存在实数a,当x∈(0,e]时,函数g(x)的最小值是3?若存在,求出a的值,若不存在,说明理由
(3)当x∈(0,e]时,求证:e2x2﹣ ![]() x>(x+1)lnx.
x>(x+1)lnx.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在![]() 轴上,离心率等于
轴上,离心率等于![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线![]() 的焦点。
的焦点。
(1)求椭圆C的标准方程。
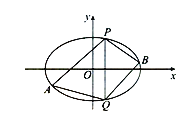
(2)已知点![]() 在椭圆C上,点A、B是椭圆C上不同于P、Q的两个动点,且满足:
在椭圆C上,点A、B是椭圆C上不同于P、Q的两个动点,且满足: ![]() 。试问:直线AB的斜率是否为定值?请说明理由。
。试问:直线AB的斜率是否为定值?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() x2﹣mlnx,g(x)=x2﹣(m+1)x,m>0.
x2﹣mlnx,g(x)=x2﹣(m+1)x,m>0.
(1)求函数f(x)的单调区间;
(2)当m≥1时,讨论函数f(x)与g(x)图象的交点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣ ![]() x3+bx2+cx+bc.
x3+bx2+cx+bc.
(1)若函数f(x)在x=1处有极值﹣ ![]() ,试确定b、c的值;
,试确定b、c的值;
(2)若b=1,f(x)存在单调递增区间,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com