



 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
16.(2)解(1)当a=1,b=-2时,g(x)=f(x)-2,把f(x)图象向下平移两个单位就可得到g(x)图象,
这时函数g(x)只有两个零点,所以(1)不对
(2)若a=-1,-2<b<0,则把函数f(x)作关于x轴对称图象,然后向下平移不超过2个单位就可得到g(x)图象,这时g(x)有超过2的零点
(3)当a<0时, y=af(x)根据定义可断定是奇函数,如果b≠0,把奇函数y=af(x)图象再向上(或向下)平移后才是y=g(x)=af(x)+b的图象,那么肯定不会再关于原点对称了,肯定不是奇函数;当b=0时才是奇函数,所以(3)不对。所以正确的只有(2)
一盒中放有大小相同的红色、绿色、黄色三种小球,已知红球个数是绿球个数的两倍,黄球个数是绿球个数的一半,现在从该盒中随机取出一球,若取出红球得1分,取出黄球得0分,取出绿球得-1分,试写出从该盒中取出一球所得分数Y的分布列.
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学选修2-3 2.1离散性随机变量分布列练习卷(解析版) 题型:解答题
一盒中放有大小相同的红色、绿色、黄色三种小球,已知红球个数是绿球个数的两倍,黄球个数是绿球个数的一半.现从该盒中随机取出一个球,若取出红球得1分,取出黄球得0分,取出绿球得-1分,试写出从该盒中取出一球所得分数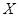 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com