
分析 通过θ所在象限,化简表达式,求解即可.
解答 解:1+sinθ$\sqrt{1-co{s}^{2}θ}+cosθ\sqrt{1-si{n}^{2}θ}$=0,
可得1+sinθ|sinθ|+cosθ|cosθ|=0,
当θ∈[2kπ,$2kπ+\frac{π}{2}$],k∈Z,上式化为:1+sin2θ+cos2θ=0,等式不成立.
当θ∈[$2kπ+\frac{π}{2}$,2kπ+π],k∈Z,上式化为:1+sin2θ-cos2θ=0,可得cos2θ=1,2θ=2kπ,θ=kπ,
可得θ=2kπ+π,k∈Z等式成立.
当θ∈[2kπ+π,$2kπ+\frac{3π}{2}$],k∈Z,上式化为:1-sin2θ-cos2θ=0,等式恒成立.
当θ∈[$2kπ+\frac{3π}{2}$,2kπ+2π],k∈Z,上式化为:1-sin2θ+cos2θ=0,cos2θ=-1,2θ=2kπ+π,θ=kπ+$\frac{π}{2}$舍去.
综上:θ∈[2kπ+π,$2kπ+\frac{3π}{2}$],k∈Z,
故答案为:[2kπ+π,$2kπ+\frac{3π}{2}$],k∈Z,
点评 本题考查三角函数的化简求值,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [1,+∞) | C. | [-1,2] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,5) | B. | (-∞,2)∪(2,3) | C. | (2,3) | D. | (-∞,2)∪(3,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
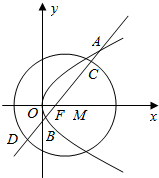 如图,抛物线C1:y2=2px(p>0)和圆C2:(x-1)2+y2=r2(r>0),M为圆C2的圆心,过抛物线C1的焦点F的直线y=k(x-$\frac{p}{2}$)与C1交于A,B两点,与圆C2交与C,D两点(点C在A,B之间)且△AOF的外心到抛物线C1的准线的距离为$\frac{3}{4}$.
如图,抛物线C1:y2=2px(p>0)和圆C2:(x-1)2+y2=r2(r>0),M为圆C2的圆心,过抛物线C1的焦点F的直线y=k(x-$\frac{p}{2}$)与C1交于A,B两点,与圆C2交与C,D两点(点C在A,B之间)且△AOF的外心到抛物线C1的准线的距离为$\frac{3}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com