
分析 (1)求导f′(x)=$\frac{1-lnx}{{x}^{2}}$,从而可得f(x)在(0,e)上单调递增,在(e,+∞)上单调递减;从而求得a≥e.
(2)可知切线l的方程为y=x-1;再令g(x)=x-1-f(x),从而可得?x>0且x≠1,g(x)>0,求导g′(x)=1-f′(x)=$\frac{{{x^2}-1+lnx}}{x^2}$,从而证明即可.
解答 解:(1)∵f(x)=$\frac{lnx}{x}$,
∴f′(x)=$\frac{1-lnx}{{x}^{2}}$,
∴f(x)在(0,e)上单调递增,在(e,+∞)上单调递减;
又∵函数y=f(x)在(a,+∞)上单调递减,
∴a≥e.
(2)证明:由(1)知,f′(1)=1,
所以l的方程为y=x-1;
令g(x)=x-1-f(x),
∵除切点外曲线C在直线l的下方,
∴?x>0且x≠1,g(x)>0,
而g(x)满足g(1)=0,且g′(x)=1-f′(x)=$\frac{{{x^2}-1+lnx}}{x^2}$,
当0<x<1时,g′(x)<0,故g(x)单调递减,
当x>1时,g′(x)>0,故g(x)单调递增;
所以对?x>0且x≠1,g(x)>g(1)=0;
所以除切点外,曲线C在直线的下方.
点评 本题考查了导数的综合应用及导数的几何意义的应用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
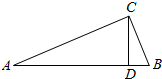
| A. | $\frac{60}{13}$ | B. | $\frac{120}{13}$ | C. | $\frac{50}{13}$ | D. | $\frac{70}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 19 | C. | 10 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7\sqrt{2}}{10}$ | B. | $\frac{\sqrt{2}}{10}$ | C. | $\frac{\sqrt{2}}{5}$ | D. | $\frac{7\sqrt{2}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com