

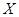 表示至第2分钟末已办理完业务的顾客人数,求
表示至第2分钟末已办理完业务的顾客人数,求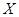 的分布列及数学期望
的分布列及数学期望科目:高中数学 来源:不详 题型:解答题
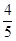 ,第二、第三种产品受欢迎的概率分别为
,第二、第三种产品受欢迎的概率分别为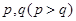 ,且不同种产品是否受欢迎相互独立.记
,且不同种产品是否受欢迎相互独立.记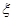 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为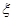 | 0 | 1 | 2 | 3 |
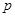 | 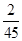 | 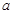 | 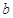 | 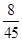 |
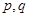 的值
的值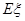 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
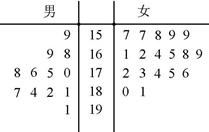
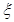 表示所选代表中女“运动健将”的人数,试写出
表示所选代表中女“运动健将”的人数,试写出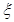 的分布列,并求
的分布列,并求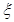 的数学期望.
的数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
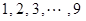 班参加高考体检,
班参加高考体检,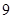 个班中,任选
个班中,任选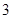 个班先参加视力检查. (I)求这
个班先参加视力检查. (I)求这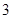 个班中恰有
个班中恰有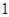 个班班级序号是偶数的概率;
个班班级序号是偶数的概率;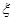 为这
为这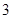 个班中两班序号相邻的组数(例如:若选出的班为
个班中两班序号相邻的组数(例如:若选出的班为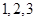 班,则有两组相邻的,
班,则有两组相邻的,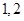 班和
班和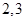 班,此时
班,此时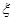 的值是
的值是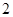 ).求随机变量
).求随机变量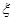 的分布列及其数学期望
的分布列及其数学期望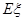 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
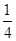 ,不堵车的概率为
,不堵车的概率为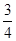 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为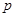 ,不堵车的概率为
,不堵车的概率为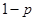 ,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为
,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为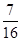 ,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数
,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数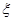 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 动作 | K | D | ||
| 得分 | 100 | 80 | 40 | 10 |
| 概率 | 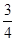 | 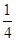 | 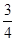 | 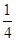 |
| 动作 | K | D | ||
| 得分 | 90 | 50 | 20 | 0 |
| 概率 | 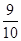 | 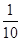 | 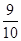 | 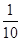 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com