
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 为正方形,
为正方形, ![]() ,
, ![]() 分别是
分别是![]() 的中点.
的中点.
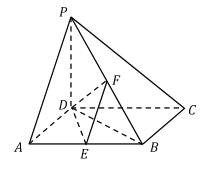
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)由题意可证得![]() ,
, ![]() ,则
,则![]() 平面
平面![]() ,由线面垂直的性质有
,由线面垂直的性质有![]() ,由三角形中位线的性质可得
,由三角形中位线的性质可得![]() ,则
,则![]()
(Ⅱ)(方法一)![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,建立空间直角坐标系,计算可得
轴,建立空间直角坐标系,计算可得
平面![]() 的一个法向量
的一个法向量![]() ,则
,则![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(方法二)由等体积法可得点![]() 到平面
到平面![]() 的距离
的距离![]() ,据此可得
,据此可得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
试题解析:
(Ⅰ)因为![]() 底面
底面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]()
又因为正方形![]() 中,
中, ![]() ,
, ![]()
所以![]() 平面
平面![]()
又因为![]() 平面
平面![]() ,所以
,所以![]()
因为![]() 分别是
分别是![]() 、
、![]() 的中点,所以
的中点,所以![]()
所以![]()
(Ⅱ)(方法一)由(Ⅰ)可知, ![]() ,
, ![]() ,
, ![]() 两两垂直,以
两两垂直,以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,设
轴,设![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
设平面![]() 的一个法向量
的一个法向量![]() ,
,
![]() ,解得
,解得![]()
![]()
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]()
(方法二)设点![]() 到平面
到平面![]() 的距离为
的距离为![]()
![]() 等体积法求出
等体积法求出![]()
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
, ![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,上顶点为
,上顶点为![]() ,若直线
,若直线![]() 的斜率为1,且与椭圆的另一个交点为
的斜率为1,且与椭圆的另一个交点为![]() ,
, ![]() 的周长为
的周长为![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() (直线
(直线![]() 的斜率不为1)与椭圆交于
的斜率不为1)与椭圆交于![]() 两点,点
两点,点![]() 在点
在点![]() 的上方,若
的上方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况,随机抽查了该市60名网友在该网店的网购金额情况,如下表:

若将当日网购金额不小于2千元的网友称为“网购达人”,网购金额小于2千元的网友称为“网购探者”.已知“网购达人”与“网购探者”人数的比例为2:3.

(1)确定![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数;若平均数和中位数至少有一个不低于2千元,则该网店当日被评为“皇冠店”,试判断该网店当日能否被评为“皇冠店”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin2x的图象向右平移φ(0<φ< ![]() )个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min=
)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min= ![]() ,则φ=( )
,则φ=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的一个焦点,过原点的直线
的一个焦点,过原点的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() ,
, ![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若![]() ,过点
,过点![]() 且不与坐标轴垂直的直线交椭圆于
且不与坐标轴垂直的直线交椭圆于![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() 的左右焦点分别为
的左右焦点分别为![]() 、
、![]() ,
, ![]() 为
为![]() 右支上的点,线段
右支上的点,线段![]() 交
交![]() 的左支于点
的左支于点![]() ,若
,若![]() 是边长等于
是边长等于![]() 的等边三角形,则双曲线的标准方程为( )
的等边三角形,则双曲线的标准方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】![]()
![]() 即双曲线的标准方程为
即双曲线的标准方程为![]() ,选A.
,选A.
【题型】单选题
【结束】
11
【题目】张师傅欲将一球形的石材工件削砍加工成一圆柱形的新工件,已知原球形工件的半径为![]() ,则张师傅的材料利用率的最大值等于(注:材料利用率=
,则张师傅的材料利用率的最大值等于(注:材料利用率=![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+cx(a>0),其图象在点(1,f(1))处的切线与直线 x﹣6y+21=0垂直,导函数
f′(x)的最小值为﹣12.
(1)求函数f(x)的解析式;
(2)求y=f(x)在x∈[﹣2,2]的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆 ![]() =l (a>b>0)的焦距为2,离心率为
=l (a>b>0)的焦距为2,离心率为 ![]() ,椭圆的右顶点为A.
,椭圆的右顶点为A.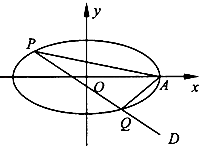
(1)求该椭圆的方程:
(2)过点D( ![]() ,﹣
,﹣ ![]() )作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的
)作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的
斜率之和为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com