
���� ���������������Ǻ�����֪ʶ�ɵ�f��x��=$\overrightarrow{m}$•$\overrightarrow{n}$=2sin��2��x+$\frac{��}{6}$������ͼ��ɵ�����T=�У��ɵæ�ֵ���ɵý���ʽ���ɵõ����������䣻
����������ɵ�A=$\frac{��}{3}$���ɵá�ABC���S=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{4}$bc���ɻ�������ʽ�ɵã�
��� �⣺����$\overrightarrow{m}$=��sin��x+cos��x��$\sqrt{3}$cos��x����$\overrightarrow{n}$=��cos��x-sin��x��2sin��x�����Ҧأ�0��
��f��x��=$\overrightarrow{m}$•$\overrightarrow{n}$=��sin��x+cos��x����cos��x-sin��x��+$\sqrt{3}$cos��x•2sin��x
=cos2��x-sin2��x+2$\sqrt{3}$cos��xsin��x=cos2��x+$\sqrt{3}$sin2��x=2sin��2��x+$\frac{��}{6}$��
��f��x����ͼ���������Գ���֮��ľ������$\frac{��}{2}$��
������T=2��$\frac{��}{2}$=����2��=$\frac{2��}{T}$=2����f��x��=2sin��2x+$\frac{��}{6}$����
��2k��-$\frac{��}{2}$��2x+$\frac{��}{6}$��2k��+$\frac{��}{2}$�ɵ�k��-$\frac{��}{3}$��x��k��+$\frac{��}{6}$��
�ຯ��f��x���ĵ���������Ϊ[k��-$\frac{��}{3}$��k��+$\frac{��}{6}$]��
����b+c=4��f��A��=2sin��2A+$\frac{��}{6}$��=1��
�����������ڽǵķ�Χ�ɵ�2A+$\frac{��}{6}$=$\frac{5��}{6}$�����A=$\frac{��}{3}$��
��ABC���S=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{4}$bc��$\frac{\sqrt{3}}{4}$��$\frac{b+c}{2}$��2=$\sqrt{3}$��
���ҽ���b=c=2ʱȡ�Ⱥţ���ʱ������Ϊ�������Σ�
���ABC��������ֵΪ$\sqrt{3}$��
���� ���⿼�����Ǻ�����ȱ任���漰�����κ����ĵ����Ժ�����Լ���������ʽ�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-1��1} | B�� | {-1��3} | C�� | {1��3} | D�� | {3��1��-1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
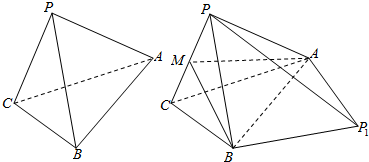 ��ͼ1��������PABC�У�BC=BP=1��AC=AP=$\sqrt{3}$��AB=2������PAB��ֱ��AB��������P1AB��ʹ��A��P1��B��C��ͬһƽ���ڣ���ͼ2������MΪPC�е㣮
��ͼ1��������PABC�У�BC=BP=1��AC=AP=$\sqrt{3}$��AB=2������PAB��ֱ��AB��������P1AB��ʹ��A��P1��B��C��ͬһƽ���ڣ���ͼ2������MΪPC�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com