
分析 (1)求出“p∧q”为真命题,实数a的取值范围
(2)结合r是¬t的必要不充分条件,可得满足条件的正整数m的值.
解答 解:(1)由3a≤9,得a≤2,即p:a≤2.
由△=9(3-a)2-4×9≤0,解得1≤a≤5,即q:1≤a≤5.
∵“p∧q”为真命题,
∴$\left\{\begin{array}{l}{a≤2}\\{1≤a≤5}\end{array}\right.$,
解得1≤a≤2.
(2)又t:a<m或$a>m+\frac{1}{2}$,从而$?t:m≤a≤m+\frac{1}{2}$.
∵r是?t的必要不充分条件,即?t是r的充分不必要条件,
∴$\left\{\begin{array}{l}m≥1\\ m+\frac{1}{2}≤2\end{array}\right.$,
解得$1≤m≤\frac{3}{2}$,
∵m∈N*,
∴m=1
点评 本题以命题的真假判断与应用为载体,考查了充要条件,函数的极值,指数不等式的解法,二次不等式的解法,复合命题,难度中档.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:2:3 | B. | sin1:sin2:sin3 | C. | 1:$\sqrt{3}$:2 | D. | 1:2:$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
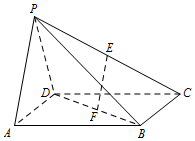 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 月份x | 1 | 2 | 3 | 4 |
| 用水量 | 4.5 | 4 | 3 | 2.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{99}$ | B. | $\sqrt{33}$ | C. | 4$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com